Рассмотрим две матрицы одинаковых размеров mn :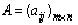,. Обозначим через I множество, состоящее из первых m чисел натурального ряда, т.е.

I = {1, 2, …, m }.

Матрицы А и В называются равными , если

,

т.e. в которых равны элементы, стоящие на одинаковых местах.

Обозначается: А = В .

Суммой матриц А и В называется матрица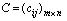, элементы которой определяются по формулам:

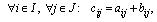
т.e. элементы матрицы С равны сумме соответствующих элементов матриц А и В .

Обозначается: С = А + В . Произведением матрицы А на действительное число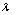 называется матрица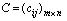, элементы которой вычисляются по формуле:

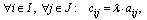
т.е. каждый элемент матрицы А умножается на число.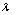

Обозначается: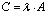.Пусть теперь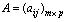, ,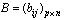 т.е. число столбцов матрицы А совпадает с числом строк матрицы В . Произведением матрицы А на матрицу В называется матрица размера mхn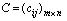, элементы которой вычисляются по формуле:

,

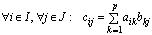
т.е. элемент матрицы С с номерами i и j равен сумме попарных произведений элементов i -й строки матрицы А на соответствующие элементы j -го столбца матрицы В (правило «строка на столбец»). Обозначается:.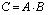

Например, если 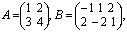то элементы матрицы 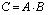будут равны:

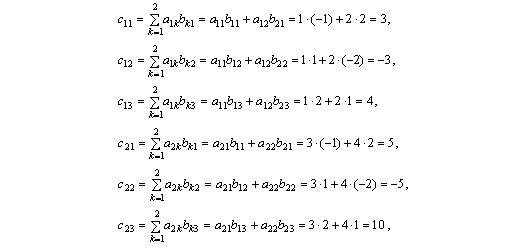
таким образом

.

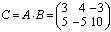
Произведение матриц не коммутативно (не перестановочно)!, т.е., вообще говоря,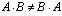. Но, если все-таки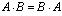, то матрицы А и В называются перестановочными .Квадратная матрица, у которой элементы, стоящие на главной диагонали равны 1, а все остальные равны 0, называется единичной и обозначается: Е .Единичная матрица перестановочна с любой квадратной матрицей порядка n , так как нетрудно убедиться, что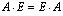.Определим понятие обратной матрицы. Оно определяется только для квадратных матриц. Далее А — квадратная матрица порядка n .Матрица 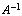называется обратной к матрице А , если

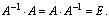
Очевидно, если 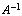— матрица обратная к А , то матрица А является обратной к 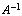(вытекает из определения, оно симметрично относительно матриц А и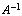), т.е. 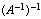= А. Поэтому матрицы А и 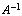называются взаимно обратными.Матрица называется невырожденной , если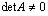, и вырожденной в противном случае.Для вырожденной матрицы обратной не существует! Получим формулу для нахождения обратной матрицы.Транспонированная матрица, составленная из алгебраических дополнений к элементам матрицы А , называется присоединенной и обозначается: А v . Таким образом, по определению

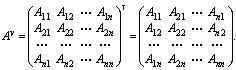
Найдем произведения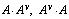. Пусть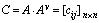, тогда

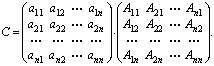
По определению произведения матриц, элементы матрицы С вычисляются по формуле:

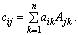
Здесь, если i = j , то по теореме о разложении определителя по строке (формула (1.6))

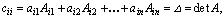
если i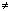 j , то по теореме аннулирования (формула (1.7))

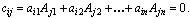
Таким образом, матрица С имеет вид:

.

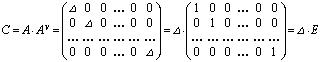
Аналогично можно показать, что 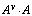= 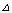Е , следовательно, выполняются равенства: = = 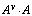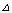Е . Если А — невырожденная матрица, т.е. 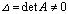, то эти равенства можно переписать в виде:

.

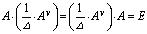
Откуда, по определению обратной матрицы, получаем:

.

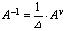
Например: если 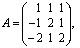то