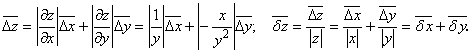Теорема 1.4. Если функция z = f(M) имеет частные производные в некоторой 
-окрестности точки М и эти производные непрерывны в самой точке М, то функция дифференцируема в точке М.
Доказательство. Придадим переменным х и у столь малые приращения 
, чтобы точка 
не выходила за пределы указанной -окрестности точки М. Полное функции Dz = f(х + Dх, у + Dу) – f(х, у) можно записать в виде
.
Выражение 
можно рассматривать как приращение функции 
одной переменной x (второй аргумент имеет постоянное значение, равное 
). Так как согласно условию эта функция имеет производную 
, то по теореме Лагранжа получаем
.
Рассуждая аналогично, для выражения 
имеем
.
Производные 
и 
непрерывны в точке М(х; у), поэтому
Отсюда следует, что
где 
– бесконечно малые при 
функции. Подставляя полученные выражения в формулу для 
, находим
Dz = 
Dх + 
Dу + 
,
а это и означает, что функция z = f(M) дифференцируема в точке М. ■
Следствие. Из непрерывности частных производных следует непрерывность самой функции.
Теорема 1.4 имеет важное значение для установления дифференцируемости функций, поскольку непосредственная проверка дифференцируемости функции с помощью определения часто затруднительна, в то время как проверка непрерывности производных оказывается проще.
В заключение заметим, что понятие дифференцируемости функции трех и более переменных вводится аналогично функции двух переменных.
Определение. Полным дифференциалом dz функции z = f(x, y) называется главная часть полного приращения Dz, линейная относительно приращений аргументов, т.е.
dz = df(x, y) = АDх + ВDу.
Дифференциалы независимых переменных совпадают с их приращениями, т.е. dx = Dх, dy = Dу.
Поэтому полный дифференциал функции z = f(х, у) вычисляется по формуле:
Полный дифференциал функции трех аргументов u = f(x, y, z) вычисляется по формуле:
При достаточно малом r = 
для дифференцируемой функции справедливо приближенное равенство Dz » dz. Учитывая, что полное приращение
Dz = f(x0 +Dх, у0 + Dу) – f(x0, у0),
получим приближенное равенство:
f(x0 +Dх, у0 + Dу) » f(x0, у0) + df(x0, у0),
которое будет тем точнее, чем меньше |Dх| и |Dу|. Этой формулой можно пользоваться для приближенных вычислений значений функции двух переменных в точке 
, если известны значения этой функции и ее частные производные в точке М0(х0, y0).
Пример 1.13. Вычислить приближенно 
.
Решение. Рассмотрим функцию z = f(x, y) = 
. Значение этой функции в точке М0(6, 8) известно и равно f(6, 8) = 
= 10.
Вычислим приближенно значение f(6,03; 8,04), имеем
f(x0 + Dх, у0 + Dу) » f(x0, у0) + df(x0, у0),
где x0 = 6, у0 = 8, Dх = 0,03; Dу = 0,04; М0(6, 8).
;
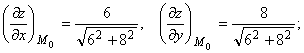
тогда
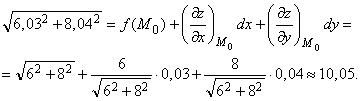
Пример 1.14. Вычислить приближенно arctg
Решение. Рассмотрим функцию z = arctg
Значение функции в точке М0(х0, y0), где х0 = 1, , y0 = 1, известно и равно arctg
Воспользуемся формулой:
f(x0 + Dх, у0 + Dу) » f(x0, y0) + dz ,
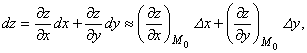при 
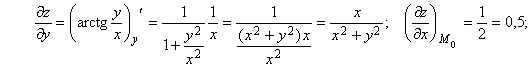
Следовательно, 
Пример 1.15. 
Найти du.
Решение. 
здесь 
Полный дифференциал применяется также в приближенных вычислениях при оценке погрешностей. Пусть задана функция z = f(х, у), причем определяемые значения x и у допускают погрешности Dх и Dy. При достаточно малых Dх и Dу приращение функции можно заменить ее дифференциалом 
. Здесь и погрешности Dх, Dу, и коэффициенты при них могут быть отрицательными и положительными. Заменим их абсолютными значениями и, учитывая свойства абсолютных величин, получим следующее неравенство:
Если через 
обозначить максимальные абсолютные погрешности (или границы для абсолютных погрешностей), то эту формулу можно записать в виде:
Относительной погрешностью называется отношение абсолютной погрешности к абсолютному значению измеряемой величины 
Максимальная относительная погрешность равна отношению максимальной абсолютной погрешности к абсолютному значению измеряемой величины 
Пример 1.16. Для вычисления объема цилиндра были вычислены его высота и диаметр основания. При этом оказалось, что высота h = 60 см, а диаметр D = 50 см. Границы ошибок, допущенных при измерении Dh = DD = 0,1 см.
Найти максимальную абсолютную погрешность вычисления объема цилиндра.
Решение. Известно, что объем цилиндра 
V = (3,14·2500·60)/4 = 117750 см3 = 117,75 дм3.
Чтобы вычислить границу ошибки в полученном результате, примем DV » dV.
Оценим абсолютную величину dV
DV 
[(3,14·2500)/4]0,1 + [(3,14·60·50)/2]0,1 = 667,25 см3 » 0,7 дм3.
Итак, границы абсолютной погрешности вычисления объема цилиндра 
дм3. Максимальная относительная погрешность
или 
= 0,59 %.
Пример 1.17. Дана функция z = х – у. Найти максимальную абсолютную погрешность.
Решение. Так как dz = 
х – Dу, то |dz| |Dх| + |Dу|.
Следовательно, 
.
Пример 1.18. Дана функция z = х/у. Найти максимальную относительную погрешность.
Решение. Максимальная абсолютная погрешность
