Рассмотрим систему n линейных уравнений c n неизвестными:

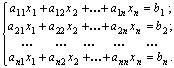
Пусть матрица системы 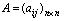является невырожденной. Обозначим через Х матрицу-столбец, составленную из неизвестных х 1 , х 2 , …, х n , и через В матрицу-столбец из свободных коэффициентов b 1 , b 2 ,…, b n , т.е.

.

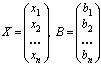
Тогда систему можно записать в матричном виде:

.

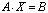
Для того чтобы найти решение системы, умножим левую и правую части последнего равенства на матрицу А — 1 слева (произведение матриц не коммутативно), получим:

.

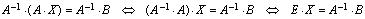
Отсюда матричное решение системы будет:

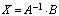
. (1.13)

Пример. 1.1. Решить систему уравнений:

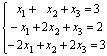
матричным способом.

Решение. Здесь матрица системы:

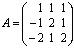
является невырожденной, и обратная к ней найдена в примере (разд. 1.5). По формуле (1.13) находим:

,

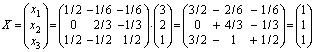
т. е. x 1 = 1, x 2 = 1, x 3 = 1 — решение системы.