Определение. Касательной плоскостью к поверхности в точке М называется плоскость, содержащая все касательные к кривым, проведенным на поверхности через точку М.
Определение. Нормалью к поверхности называется прямая, проходящая через точку касания М и перпендикулярная касательной плоскости.
Если поверхность задана уравнением F(x, y, z) = 0, т.е. в неявном виде, то уравнение касательной плоскости в точке М0(х0, у0, z0) поверхности имеет вид:
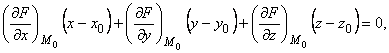
где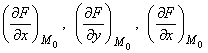 
– значения частных производных в точке М0,
а х, у, z – текущие координаты точки касательной плоскости.
Если обозначить частные производные через 
то уравнение касательной плоскости может также быть записано в следующем виде:
.
Уравнения нормали:
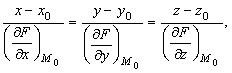
где х, у, z – текущие координаты точки нормали.
Если же уравнение поверхности задано в явном виде 
, то уравнение касательной плоскости в точке М0(х0, у0, z0) имеет вид
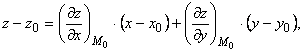
а уравнения нормали
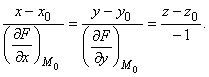
Пример 1.19. Дана поверхность 
и на ней точка М0(1, 1, 1). Составить уравнение касательной плоскости и уравнения нормали в точке М0.
Решение. Находим частные производные
и их значения в точке M0(1, 1, 1):
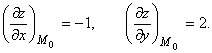
Уравнение касательной плоскости:
z – 1 = –(х – 1) + 2(у – 1) или х – 2у + z = 0.
Уравнения нормали: