Рассмотрим прямоугольную матрицу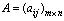 . Выберем в матрице А произвольно k строк с номерами i 1 , i 2 , … , i k и k столбцов с номерами j 1 , j 2 , … , j k ,
. Выберем в матрице А произвольно k строк с номерами i 1 , i 2 , … , i k и k столбцов с номерами j 1 , j 2 , … , j k , 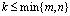 . Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу А k порядка k .
. Элементы, стоящие на пересечении выбранных строк и столбцов, образуют квадратную матрицу А k порядка k .
Определитель матрицы А k называется минором k -гo порядка (минором порядка k ) и обозначается 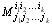 или, когда не важно, какие именно строки и столбцы выбраны, обозначается M k , т.е. по определению M k = det А k . Например, если
или, когда не важно, какие именно строки и столбцы выбраны, обозначается M k , т.е. по определению M k = det А k . Например, если
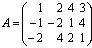
и выбраны строки c номерами i 1 = 1, i 2 = 3 и столбцы с номерами j 1 = 2, j 2 = 4, то
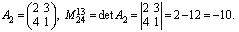
Число миноров второго порядка для этой матрицы равно 18.
Наивысший порядок миноров, не равных нулю, называется рангом матрицы и обозначается символами: rаng А или r A .
Из этого определения легко получить следующее правило для нахождения ранга матрицы: если найден минор порядка r не равный нулю и любой минор порядка r + 1 равен нулю, то ранг матрицы А равен r .
Пример 1.2 . Найти ранг матрицы:
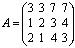
.
Решение. Здесь 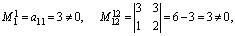
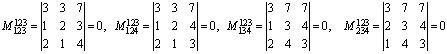
,
следовательно rаng А = 2.
Вычисление ранга матрицы по определению приводит к очень громоздким и длительным вычислениям, поэтому чаще всего он вычисляется с помощью элементарных преобразований матрицы.
Элементарные преобразования матрицы:1) перестановка (транспозиция) строк (столбцов) матрицы;2) умножение всех элементов отроки (столбца) матрицы на действительное число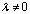 ;3) прибавление к элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на действительное число. Утверждение 1.4 Элементарные преобразования не изменяют ранга матрицы. Доказательство. Действительно, из свойств определителей получаем, что при преобразовании 1 определитель изменяет знак на противоположный (свойство 1°). При преобразовании 2 определитель умножается на число
;3) прибавление к элементам строки (столбца) матрицы соответствующих элементов другой строки (столбца), умноженных на действительное число. Утверждение 1.4 Элементарные преобразования не изменяют ранга матрицы. Доказательство. Действительно, из свойств определителей получаем, что при преобразовании 1 определитель изменяет знак на противоположный (свойство 1°). При преобразовании 2 определитель умножается на число 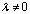 (свойство 5°). И при преобразовании 3 определитель не изменяется (свойство 8°). Следовательно, если
(свойство 5°). И при преобразовании 3 определитель не изменяется (свойство 8°). Следовательно, если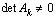 , то после преобразований 1, 2 или 3 он останется не равным 0; если det A k = 0, то после преобразований он по-прежнему будет равен 0.Матрицы, полученные одна из другой с помощью элементарных преобразований, называются эквивалентными . Если А и В — эквивалентные матрицы, то будем писать А ~ В .При вычислении ранга матрицы с помощью элементарных преобразований матрица приводится к упрощенной (трапециевидной) форме:
, то после преобразований 1, 2 или 3 он останется не равным 0; если det A k = 0, то после преобразований он по-прежнему будет равен 0.Матрицы, полученные одна из другой с помощью элементарных преобразований, называются эквивалентными . Если А и В — эквивалентные матрицы, то будем писать А ~ В .При вычислении ранга матрицы с помощью элементарных преобразований матрица приводится к упрощенной (трапециевидной) форме:

где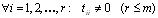 . Тогда rang T = r , так как
. Тогда rang T = r , так как
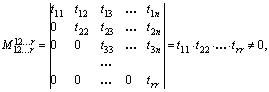
а любой минор порядка r + 1 будет равен 0, так как содержит, по крайней мере, одну строку, все элементы которой равны 0 (свойство определителей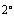 ). По утверждению (1.4) rang A = rang T , следовательно, rang A = r .
). По утверждению (1.4) rang A = rang T , следовательно, rang A = r .
Таким образом, ранг матрицы А равен числу ненулевых строк трапециевидной матрицы Т , эквивалентной матрице А .