Рассмотрим систему линейных уравнений (1.11). К матрице системы 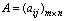допишем справа столбец из свободных членов системы b 1, b 2, … , b m , получим новую матрицу, которая называется расширенной матрицей системы и обозначается: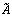, т.е.

Элементарным преобразованиям расширенной матрицы системы (cм. разд. 1.7) соответствуют эквивалентные преобразования системы линейных уравнений (1.11) (см. разд. 1.4), поэтому решение системы с помощью эквивалентных преобразований можно заменить на приведение расширенной матрицы с помощью элементарных преобразований к более простой форме. Метод Гаусса состоит из двух частей — прямого и обратного хода. Идея прямого хода метода — с помощью элементарных преобразований привести расширенную матрицу к виду, в котором матрица системы имеет трапециевидную форму.

Прямой ход метода Гаусса

Шаг 1 . Если а 11 = 0, то с помощью преобразования 1 добиваемся, чтобы на место этого элемента попал ненулевой элемент (при применении этого преобразования к столбцам матрицы исключением является последний столбец, он должен оставаться неподвижным). Если в матрице нет ненулевых элементов, то она имеет трапециевидную форму, и прямой ход завершен. Пусть 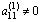(верхний индекс указывает на номер шага), умножим элемент первой строки на число 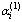и прибавим к соответствую

щим элементам i -й строки i = 2, 3, …., m . Числа 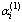подберем так, чтобы первые элементы в строках обратились в 0, т.е.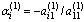. В результате получим матрицу, в которой в первом столбце под главной диагональю все элементы равны 0. Обозначим полученную матрицу:

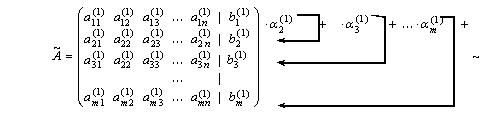
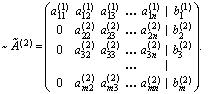
Шаг 2 . Если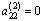, то с помощью преобразования 1 добиваемся, чтобы на место этого элемента попал ненулевой элемент матрицы. Если в этой матрице нет ненулевых элементов, то она имеет трапециевидную форму, и прямой ход завершен. Пусть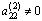, умножим элементы второй строки на число 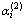и прибавим к соответствующим элементам i -й строки i = 3, 4, …, m . Числа 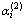подберем так, чтобы вторые элементы в строках обратились в нули, т.е.:

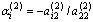В результате, получим матрицу, в которой во втором столбце под главной диагональю все элементы равны нулю.Будем выполнять указанные преобразования до тех пор, пока матрица системы А не примет трапециевидную форму, пусть это произойдет на шаге r , т.е.

.

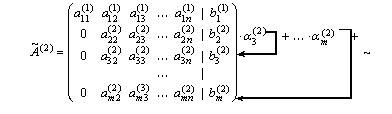
Этой матрице соответствует система уравнений, эквивалентная исходной (1.11), вида:

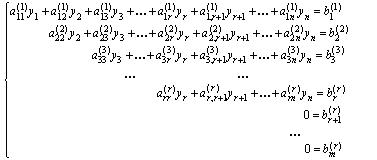
. (1.14)

Здесь неизвестные обозначены: y 1 , …, y n , потому что при применении элементарного преобразования 1 к столбцам расширенной матрицы естественный порядок переменных х 1 , х 2 …, х n нарушается. Например, если в расширенной матрице поменяли местами столбцы с номерами k и р , то в системе на месте слагаемых с номерами неизвестных k будут слагаемые с номерами неизвестных р и наоборот, т.е. у k = x p и у p = х k . На этом прямой ход метода Гаусса заканчивается. Теорема 1.2 (Кронекера-Капелли) Для того чтобы система (1.11) была совместной, необходимо и достаточно, чтобы rang A = rang.

Доказательство. При помощи прямого хода метода Гаусса, приведем систему (1.11) к виду (1.14).

Необходимость. Если система (1.11), совместна, то и система (1.14) тоже совместна, тогда

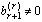
(если это не так, например,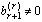 , то ( r + 1)-е уравнение 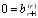не имеет решений, т.е. система несовместна, что противоречит условию). Откуда следует, что в трапециевидных матрицах, эквивалентных матрице системы и расширенной матрице (первая получается из второй удалением последнего столбца), содержится одинаковое число ненулевых строк, значит rang A = rang.

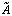Достаточность. Если rang A = rang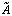, то (если это не так, например 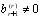, то у матрицы, эквивалентной матрице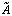, будет хотя бы на одну ненулевую строку больше, чем в матрице, эквивалентной матрице А , т.е. rang A < rang,

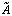что противоречит условию). Отбросим последние m — r уравнений в системе (1.14), получим систему r уравнений, которая будет эквивалентна системе (1.14), а значит и системе (1.11) (так как последние уравнения превращаются в тождества 0 = 0).Назовем неизвестные у 1 , y 2 , …, у r базисными, а у r +1 , у r +2 ,…, у n свободными и перенесем слагаемые, содержащие свободные неизвестные, в правую часть уравнений. Получим систему относительно базисных неизвестных:

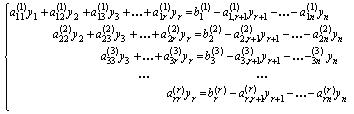
, (1.15)

которая эквивалентна (1.11), и для каждого набора значений свободных неизвестных yr +1 = t 1 , y r +2 = t 2 , …, y n = t n- r по теореме 1.1 имеет единственное решение.

Обратный ход метода Гаусса Шаг 1 . Из последнего уравнения системы (1.15) находим у r , подставив вместо свободных неизвестных произвольные числа 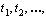t n-r :

Шаг 2. Подставляем найденный у r в предпоследнее уравнение и находим y r -1 :

. . .

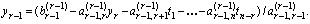
Шаг 3. Подставляем найденные у r , …, у 2 в первое уравнение находим у 1 :

В результате, получаем решение системы (1.11), в котором базисные переменные выражены через свободные переменные. Замечание. Из доказательства теоремы Кронекера-Капелли следует, что:

· если rang A = rang 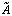= n , то система совместна и имеет единственное решение; · если rangA = rang 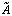< n , то система совместна и имеет бесконечное множество решений; · если rangA < rang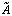, то система несовместна. Пример 1.3. Решить систему линейных уравнений:

.

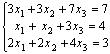
Решение. Приведем расширенную матрицу системы:

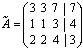
к трапециевидной форме. Поменяем местами первую и вторую строки матрицы, затем умножим элементы первой строки на — 3 и прибавим к элементам второй сроки, элементы первой строки умножим на — 2 и прибавим к элементам третьей строки, получим:

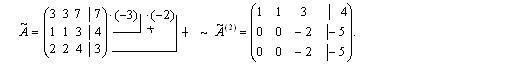
Полученная матрица не является трапециевидной, так как на главной диагонали есть элемент, равный нулю. Поменяем местами второй и третий столбцы матрицы, затем умножим элементы второй строки на — 1 и прибавим к элементам третьей строки, получим:

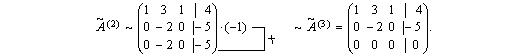
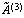Матрица имеет трапециевидную форму, причем в полученных матрицах по две ненулевых, строки, т.е. rang A = rang = 2 , следовательно, по теореме Кронекера-Капелли система совместна и имеет бесконечное множество решений. Полученной матрице соответствует система уравнений, эквивалентная исходной:

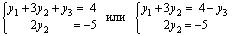
где y 1 = x 1, y 2 = x 3, y 3 = x 2, (второй и третий столбцы в расширенной матрице менялись местами). Пусть у 3 = t , тогда из второго уравнения находим у 2 = 2,5 и, подставляя у 2 в первое уравнение, получим у 1 = — 3,5 — t . Таким образом, решением данной системы уравнений будут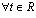: х 1 = — 3,5 — t , х 2 = t , x 3 = 2,5.