Множество L называется линейным пространством , а его элементы — векторами (будем обозначать их с чертой сверху), если:1) определена операция сложения, которая 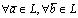 ставит в соответствие элемент
ставит в соответствие элемент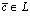 , называемый суммой, который обозначается
, называемый суммой, который обозначается 2) определена операция умножения на число, которая
2) определена операция умножения на число, которая 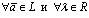 ставит в соответствие элемент
ставит в соответствие элемент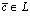 , называемый произведением вектора
, называемый произведением вектора 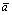 на число
на число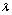 , который обозначается
, который обозначается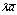 ;3)
;3)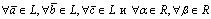 выполняются следующие аксиомы:
выполняются следующие аксиомы:
1°.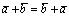 ;2о.
;2о.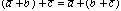 ; 3°. существует единственный вектор
; 3°. существует единственный вектор 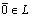 такой, что
такой, что 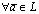 справедливо равенство:
справедливо равенство: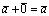 ;4°.
;4°.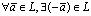 такой, что ;
такой, что ;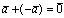 ;5°.
;5°.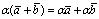 ;6°.
;6°.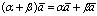 ;7°.
;7°.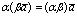 ;8°.
;8°.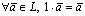 .
.
Вектор 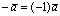 называется противоположным вектору
называется противоположным вектору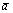 . Вектор
. Вектор 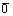 называется нулевым вектором. Сумма векторов
называется нулевым вектором. Сумма векторов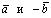 называется разностью и обозначается:
называется разностью и обозначается: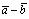 .Выражение вида
.Выражение вида 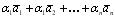 называется линейной комбинацией векторов
называется линейной комбинацией векторов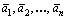 . Линейная комбинация векторов называется тривиальной, если
. Линейная комбинация векторов называется тривиальной, если
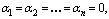
и нетривиальной, если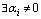 . Далее будем использовать факт, что
. Далее будем использовать факт, что
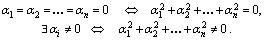
Система векторов 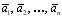 называется линейно зависимой , если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору.Если равенство нулевому вектору возможно лишь для тривиальной линейной комбинации, то система векторов
называется линейно зависимой , если существует нетривиальная линейная комбинация этих векторов, равная нулевому вектору.Если равенство нулевому вектору возможно лишь для тривиальной линейной комбинации, то система векторов 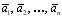 называется линейно независимой . Таким образом:
называется линейно независимой . Таким образом:
система векторов линейно зависима, если 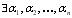 такие, что
такие, что
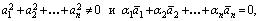
система векторов линейно независима, если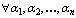 справедливо
справедливо
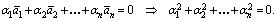
Утверждение 1.5. Система из n (n > 1) ненулевых векторов линейно зависима тогда и только тогда, когда хотя бы один из векторов является линейной комбинацией остальных.
Доказательство Необходимость. Так как система векторов линейно зависима, то 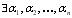 такие, что
такие, что
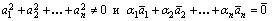
.
Пусть, например, а i = 0, тогда
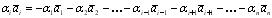
или,
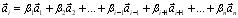
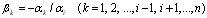
Таким образом, вектор 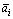 является линейной комбинацией остальных n — 1 векторов. Достаточность. Пусть, например,
является линейной комбинацией остальных n — 1 векторов. Достаточность. Пусть, например,
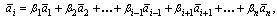
перенесем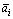 , в правую часть равенства и получим нетривиальную линейную комбинацию векторов (так как
, в правую часть равенства и получим нетривиальную линейную комбинацию векторов (так как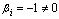 ), равную.
), равную.
Базисом в линейном пространстве L называется любая упорядоченная система векторов, обладающая следующими свойствами:
· она линейно независима; · любой вектор из L является линейной комбинацией векторов этой системы.
Пусть таких векторов в системе n штук. Обозначим эти векторы: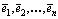 . Коэффициенты линейной комбинации векторов, о которой идет речь в определении (свойство б), называются координатами вектора в базисе
. Коэффициенты линейной комбинации векторов, о которой идет речь в определении (свойство б), называются координатами вектора в базисе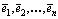 , т.е., если
, т.е., если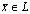 , то
, то
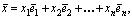
и тогда 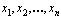 — координаты вектора x в базисе
— координаты вектора x в базисе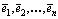 . Обозначим через Х матрицу-столбец, состоящую из координат вектора x, через e — матрицу-строку, состоящую из векторов базиса
. Обозначим через Х матрицу-столбец, состоящую из координат вектора x, через e — матрицу-строку, состоящую из векторов базиса , тогда
, тогда 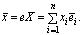
Утверждение 1.6 Координаты любого вектора определяются в базисе e однозначно.
Доказательство. Пусть тогда
тогда
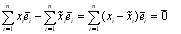
.
Так как система векторов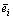 линейно независима, то все коэффициенты полученной линейной комбинации равны 0, т.е.
линейно независима, то все коэффициенты полученной линейной комбинации равны 0, т.е.
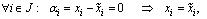
следовательно, координаты вектора x определяются однозначно.