11.2. Календарное планирование | Электронная библиотека

Естественные науки / Математика. Экономико-математические методы / 11.2. Календарное планирование

Применение методов СПУ должно обеспечить получение календарного плана, определяющего сроки начала и окончания каждой операции.

В результате вычислений определяются критические и некритические операции.

Операция считается критической, если задержка ее начала приводит к увеличению срока окончания всей программы.

Некритическая операция отличается тем, что промежуток времени между ее ранним началом и поздним окончанием больше ее фактической продолжительности, т.е. операция имеет резерв, или запас времени.

Критический путь определяет непрерывную последовательность критических операций, связывающих исходное и завершающее события программы (сети). Критический путь определяет минимальный срок выполнения всей программы в целом. Поэтому нахождению критического пути придается очень большое значение.

Обозначим:

– длительность операции ;

– ранний срок начала всех операций, выходящих из события (момент окончания всех операций, входящих в событие );

– поздний срок окончания всех операций, входящих в событие (ранний срок начала всех операций, выходящих из события ), тогда для всех операций справедливы равенства:

, (11.1)

. (11.2)

С использованием этих формул рассчитывается критический путь программы. Расчет включает два этапа.

Первый этап – прямой ход

Вычисления начинаются с исходного события и продолжаются до тех пор, пока не будет достигнуто завершающего события всей сети.

Для каждого события вычисляется одно число, представляющее ранний срок его наступления (момент завершения всех операций, входящих в это событие (формула 11.1)).

Второй этап – обратный ход

Вычисления начинаются с завершающего события сети и продолжаются до тех пор, пока не будет достигнуто исходного события.

Для каждого события вычисляется число, представляющее поздний срок его наступления по формуле 11.2.

Операция принадлежит критическому пути, если она удовлетворяет следующим четырем условиям:

, , .

Резервы времени

При определении критического пути необходимо вычислить резервы времени для некритических операций. Определим сроки позднего начала – и раннего окончания – операции по формулам:

(рис. 11.6, а); (рис. 11.6, б).

Различают два вида резервов времени для некритических операций:

· полный резерв времени – ;

· свободный резерв времени – .

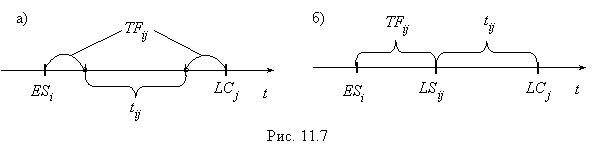
Полный резерв времени операции представляет собой разность между максимальным отрезком времени, в течение которого может быть выполнена операция , и ее продолжительностью. Т.е.

(рис. 11.7, а); (рис. 11.7, б)

( – промежуток времени, в течение которого может быть выполнена операция).

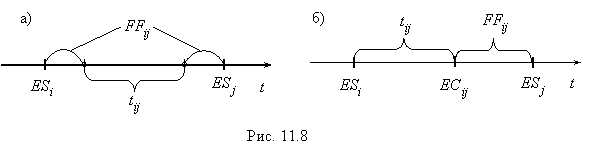
Свободный резерв времени определяется аналогично, но в предположении, что все операции в сети начинаются в ранние сроки. При этом свободный резерв времени определяется как превышение отрезка времени между ранними сроками событий i и j над длительностью операции . Т.е.

(рис. 11.8, а); (рис. 11.8, б).

Свободный резерв времени всегда меньше полного резерва времени либо равен ему.

Рассмотрение основных понятий и положений СПУ будем вести на основе следующего примера.

Пример 10.2

Пусть задана следующая последовательность работ с их временными характеристиками (табл. 11.1):

Таблица 11.1

Работа	Длительность	Работа	Длительность	Работа	Длительность	Работа	Длительность
1 – 2	10	3 – 6	8	5 – 7	6	7 – 10	6
1 – 3	4	4 – 5	3	6 – 7	9	8 – 10	9
1 – 4	6	4 – 6	10	6 – 9	7	9 – 10	11
2 – 5	9	4 – 7	4	7 – 8	12
3 – 4	7	5 – 8	5	7 – 9	8

Требуется: построить сетевой график; найти критический путь; определить полные и свободные резервы времени некритических операций.

Решение. Построим сетевой график так, чтобы все дуги – работы были направлены слева направо (рис. 11.9). Над дугами проставим длительности работ.

Критический путь на сетевом графике представляет собой путь от начальной до конечной работы, имеющей наибольшую длительность – минимальный срок выполнения всей программы в целом. Любое замедление в выполнении работ критического пути неизбежно приведет к замедлению выполнения всего комплекса работ, поэтому критическому пути и уделяется столько внимания.

Первый этап – прямой ход

Находим ранние сроки всех событий по формуле (11.1). Считаем, что .

Событиям 2 и 3 предшествуют только работы (1, 2) и (1, 3) соответственно, поэтому (из 1), (из 1) (в скобках указаны начальные события критических операций для восстановления критического пути после вычислений).

Далее последовательно, в соответствие с общей формулой (11.1), находим:

(из 3);

(из 2);

(из 4);

(из 6);

(из 7);

(из 8).

Теперь легко находим критический путь (события критического пути подчеркнуты). Таким образом, критический путь состоит из работ:

(1, 3) – (3, 4) – (4, 6) – (6, 7) – (7, 8) – (8, 10)

и его длительность – 51 (рис. 11.10). На рис. 11.10 операции и события критического пути выделены жирными линиями.

Второй этап – обратный ход

Определяем поздние сроки всех событий по формуле (11.2).

Здесь считаем, что , т.е. . Таким образом, находим:

; ;

;

; ;

Над каждым из событий запишем дробь, в числителе которой проставим ранний срок начала операций, выходящих из этого события, а в знаменателе – поздний срок окончания операций, входящих в это событие.

Таким образом, получим:

1) ранние сроки наступления событий (числители дробей);

2) поздние сроки наступления событий (знаменатели дробей);

3) резервы времени событий (разность между знаменателями и числителями). В нашем случае критическими событиями (не имеющими резервов) являются 1, 3, 4, 6, 7, 8, 10. Продолжительность критического пути равна 51 (числитель или знаменатель последнего события);

4) поздние сроки начала работ (i, j) (знаменатели дробей конечных событий за вычетом длительностей работ);

5) ранние сроки окончания работ (i, j) (суммы числителей начальных событий и длительностей работ);

6) общие резервы времени работ (разности между знаменателем конечных событий и числителем начальных событий за вычетом длительностей работ);

7) свободные резервы времени работ (разности между числителями начальных и конечных событий за вычетом длительностей работ).

Резерв времени события определяется как разность между их ES и LC. Соответственно, резервы времени событий вдоль критического пути равны нулю. Для нашего примера, резерв времени например, события 2 будет: 15 – 10 = 5, а резерв времени события 9 будет: 40 – 38 = 2. На этот промежуток времени может быть задержано выполнение соответствующей работы без риска задержать проект в целом.

Если свободные резервы времени работ могут быть использованы по всем работам сети одновременно (тогда все работы становятся критическими), то для полных резервов этого сказать нельзя; его можно использовать или для одной работы пути полностью, или для разных работ частями.

Для критических работ и равны нулю, и могут быть использованы при выборе календарных сроков выполнения некритических работ и для частичной оптимизации сетевых графиков.

Временные характеристики некритических работ приведены в табл. 11.2.

Таблица 11.2

Некритические работы

Продолжительность

Ранние сроки начала работ

Поздние сроки окончания работ

Ранние сроки окончания работ

Поздние

сроки начала работ

Общий

резерв

времени

Свободный

резерв

времени

1 – 2

1 – 4

2 – 5

3 – 6

4 – 5

4 – 7

5 – 7

5 – 8

6 – 9

7 – 9

7 – 10

9 – 10