Кривые безразличия отражают систему предпочтений индивида, но для анализа потребительского выбора необходимо учесть еще две важные переменные: доход потребителя и цены товаров. Кривые безразличия лишь показывают возможность замены для индивида одного блага другим без ущерба для его благополучия. Но они не определяют, какой именно набор товаров потребитель считает для себя наиболее выгодным. Для этого вводится понятие бюджетного ограничения. Оно показывает, какое количество благ (какие потребительские наборы) можно приобрести при данных ценах и доходе.

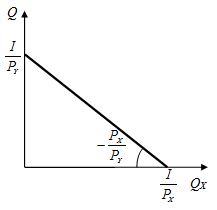
Рис. 2.18. Бюджетная линия

Предположим, что весь свой доход потребитель тратит на приобретение двух товаров X и Y. Тогда сумма его расходов на данные товары равна его доходу (бюджету), и уравнение бюджетного ограничения можно представить следующим образом:

,                                                  (2.14)

где I – доход потребителя; P_X – цена товара X; P_Y – цена товара Y; x – количество приобретенного блага X; y – количество купленного блага Y.

Бюджетная линия – это прямая, точки которой показывают различные комбинации двух товаров при равенстве расходов на их приобретение (рис. 2.18).

Бюджетная линия обладает следующими свойствами:

1) бюджетная линия характеризуется отрицательным наклоном, так как увеличение закупок одного товара возможно лишь путем сокращения расходов на другой товар;

2) точка пересечения бюджетной линии с осью абсцисс соответствует максимально возможному объему потребления продукта X. Точка пересечения бюджетной линии с осью ординат отвечает максимально возможному объему потребления продукта Y;

3) наклон бюджетной линии к осям координат определяется отношением цен продуктов. Он является величиной постоянной, поскольку потребитель не в состоянии повлиять на цены;

4) при увеличении дохода потребителя бюджетная линия сдвигается параллельно самой себе вправо (из положения AB в положение A₂B₂), а при уменьшении дохода – влево в положение A₁B₁ (рис. 2.19, а). При этом угол наклона бюджетной линии не меняется;

5) При изменении цены одного из благ меняется наклон бюджетной линии (при увеличении цены наклон становится круче, при уменьшении цены – более пологим):

а) увеличение цены товара X (P_Y = const) приведет к повороту бюджетной линии по часовой стрелке (влево) вокруг точки пересечения линии бюджетного ограничения с осью ординат (из положения AB в положение A₁B) и наоборот (см. рис. 2.19, б);

а) при увеличении цены товара Y (P_X = const) бюджетная линия повернется против часовой стрелке (влево) вокруг точки пересечения линии бюджетного ограничения с осью абсцисс (из положения AB в положение AB₁) и наоборот (см. рис; 2,19, в);

1) наборы, находящиеся слева от бюджетной линии, доступны для потребителя, а находящиеся справа – недоступны.

Рис. 2.19. Сдвиги бюджетной линии под влиянием изменения дохода и цен

Цель потребителя – сделать покупки таким образом, чтобы обеспечить себе максимум полезности в рамках своего бюджетного ограничения.

Равновесный (оптимальный) набор товаров – это набор на бюджетной линии, который обеспечивает потребителю максимальную полезность.

С формальной точки зрения решение проблемы равновесия состоит в поиске пары чисел (x;y), которая удовлетворяет бюджетному ограничению (см. формулу (2.14)) и максимизирует функцию полезности TU. Для этого необходимо совместить карту безразличия с бюджетной линией потребителя II (рис. 2.20). Это вполне правомерно, так как оси координат карты безразличия и линии бюджетного ограничения являются идентичными.

Рис. 2.20. Равновесное положение потребителя

Точка L на кривой безразличия U₃ характеризует такой набор товаров X и Y, который в данный момент (при заданном бюджете) является недоступным потребителю (хотя весьма желаемым).

Бюджетная линия II имеет три точки соприкосновения с кривыми безразличия. Рассмотрим их и определим точку равновесия.

В точках M и N, расположенных на кривой U₁, потребитель не достигнет состояния равновесия, так как, двигаясь от них влево вверх или вправо вниз соответственно, он может перейти на кривую безразличия, находящуюся выше (U₂) и характеризующую более высокий уровень совокупной полезности. Таким образом, оптимальным для потребителя будет товарный набор в точке K, которая является единственной точкой соприкосновения кривой безразличия U₂ и линии бюджетного ограничения II.

Следовательно, равновесие потребителя достигается в точке, в которой бюджетная линия касается наиболее высокой из всех доступных потребителю кривых безразличия. Стоит также отметить, что в точке равновесия K выполняется условие, названное нами ранее как правило максимизации полезности (2.11).

Примеры решения типовых задач

Задача 1

Функции совокупной полезности покупателя от потребления двух благ – хлеба (X) и мяса (Y) – заданы уравнениями:

;

,

где Q_X – количество хлеба, кг; Q_Y – количество мяса, кг.

Цена хлеба равна 2 ден. ед., а цена мяса – 5 ден. ед. Ежемесячный доход потребителя, расходуемый на эти два товара, составляет 39 ден. ед. Определите:

1) объем мяса и хлеба, приобретение которых позволит потребителю максимизировать совокупную полезность от потребления данных товаров;

2) величину максимальной общей полезности (TU_max).

Решение:

Согласно правилу максимизации полезности (2.11), наибольшую полезность обеспечивает такая структура покупок, при которой отношение предельной полезности блага (MU) к его цене (P) одинаково для всех благ. В нашем случае:

Определим функции предельной полезности для мяса и хлеба. Функция предельной полезности вычисляется как частная производная от функции общей полезности:

.

Тогда:

;

Подставив полученные выражения в уравнение максимизации полезности, получим:

или

Выбор потребителя ограничен его бюджетом. Уравнение бюджетного ограничения имеет вид:

.

Тогда:

Составим систему уравнений и найдем Q_X и Q_Y:

;

.

Отсюда

Q_X =7;                        Q_Y = 5.

Следовательно, потребляя в месяц 7 кг хлеба и 5 кг мяса, покупатель максимизирует совокупную полезность:

.

При этом он расходует весь доход:

Определим величину общей полезности для набора (7; 5):

.

Тогда:

Таким образом, потребителю необходимо приобрести 7 кг хлеба и 5 кг мяса, чтобы максимизировать совокупную полезность от потребления данных товаров, и величина максимальной общей полезности (TU_max) составит 125,5 ютилей.

Задача 2

Потребитель приобретает два товара: хлеб и молоко. Данные о количестве и полезности приобретаемых благ представлены в таблице 2.2. Цена хлеба 20 р./кг, цена молока

40р./кг. Доход потребителя составляет 220 р. Определите равновесный набор хлеба и молока, максимизирующий совокупную полезность потребителя. Изобразите ситуацию равновесия графически.

Таблица 2.2 Данные о количестве и полезности приобретаемых благ

Количество приобретаемых благ Q, кг	Общая полезность, ютили
	хлеба (TUХ)	молока (TUМ)
1	15	12
2	25	23
3	33	33
4	40	40
5	45	46

Решение:

Для определения оптимального (равновесного) набора товаров необходимо воспользоваться правилом максимизации полезности (2.11), которое в данном случае будет иметь следующий вид:

где MU_Х и MU_М – предельные полезности хлеба и молока соответственно; P_Х и P_М – цены соответственно хлеба и молока.

Рассчитаем предельные полезности двух товаров, используя формулу (2.9):

Так как в данном случае объем товаров изменяется каждый раз на постоянную величину, то знаменатель в данной формуле можно принять равным единице и при расчетах не учитывать.

Затем рассчитаем величину предельной полезности, приходящуюся на один рубль  для хлеба и молока и сведем все полученные результаты в таблицу 2.3.

Необходимо найти такое соотношение двух товаров, которое бы удовлетворяло правилу максимизации полезности. Анализ данных таблицы 2.3 показывает, что потребление 5 кг хлеба и 3 кг молока принесет потребителю наибольшее удовлетворение, так как такая комбинация соответствует правилу ().

Таблица 2.3 Результаты расчётов

Количество приобретаемых благ (Q), кг	Хлеб			Молоко
	TUХ, ютили	MUХ, ютили	ютили на рубль	TUМ, ютили	MUМ, ютили	ютили на рубль
1	15	15		12	12
2	25	25 – 15 = 10		23	23 – 12 = 11
3	33	33 – 25 = 8		33	33 – 23 = 10
4	40	40 – 33 = 7		40	40 – 33 = 7
5	45	45 – 40 = 5		46	46 – 40 = 6

Определим, доступен ли данный набор потребителю при имеющемся бюджете в 220 р. Для этого используем уравнение бюджетного ограничения (2.14), подставив в него имеющиеся данные:

Данный набор доступен потребителю, при этом весь бюджет последнего будет израсходован. Таким образом, данный набор хлеба и молока полностью соответствует правилу максимизации полезности.

Для изображения ситуации равновесия потребителя графически необходимо на одном графике совместить бюджетную линию и кривую безразличия.

Для построения бюджетной линии достаточно определить координаты двух точек. Определим максимальное количество хлеба  и молока , которые может приобрести потребитель на свой бюджет:

Рис. 2.21. Равновесие потребителя

Расположим точки с координатами (11; 0) и (0; 5,5) на осях абсцисс и ординат соответственно и построим линию бюджетного ограничения (рис. 2.21). Также возьмем точку, принадлежащую данной линии с координатами (5; 3) и проведем через нее кривую безразличия (произвольной формы).

Задания для самоконтроля

1. Какое из следующих утверждений является неправильным?

а) Каждая точка на кривой безразличия означает определённую комбинацию двух товаров.

б) Каждая точка на бюджетной линии означает определённую комбинацию двух товаров.

в) Все точки на кривой безразличия означают одинаковый уровень удовлетворения потребностей.

г) Все точки на кривой безразличия означают одинаковый уровень денежного дохода.

2. Установите соответствие между приведенными терминами и определениями:

Термины	Определения
1. Предельная полезность	а) пропорция, в соответствии с которой одно благо может быть замещено другим без выигрыша или потери для удовлетворения потребителя
2. Карта кривых безразличия	б) приращение общей полезности при увеличении потребления блага на единицу
3. Предельная норма замещения	в) совокупность точек, представляющих различные сочетания двух благ, доступных потребителю при данных ценах и бюджете
4. Принцип убывающей предельной полезности	г) при заданных ценах и бюджете потребитель достигает максимума полезности тогда, когда отношение предельной полезности к цене одинаково для всех потребляемых благ
5. Линия бюджетного ограничения	д) метод описания предпочтений потребителя совокупностью его кривых безразличия
6. Принцип максимизации полезности	е) по мере увеличения потребления блага, предельная полезность каждой дополнительной единицы блага сокращается

1. Еженедельный доход потребителя составляет 200 ден. ед. Используя бюджетные линии и соответствующие им кривые безразличия (рис. 2.22), определите цену товара Y, а также цены товара X до и после изменения.

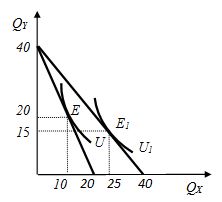
Рис. 2.22. Бюджетные линии и соответствующие им кривые безразличия

2. Если потребитель выбирает комбинацию, представленную точкой, лежащей на плоскости, ограниченной бюджетной линией, то он:

а) максимизирует полезность;

б) желает купить больше товаров, чем позволяет его бюджет;

в) не полностью использует свой бюджет;

г) находится в положении потребительского равновесия.

3. Заданы равновесные объемы потребления продуктов X и Y при некоторых значениях дохода потребителя (табл. 2.4). Цены продуктов неизменны. Определите цены товаров и заполните пустые ячейки таблицы.

Таблица 2.4 Равновесные объемы потребления продуктов X и Y при некоторых значениях дохода потребителя

Доход потребителя I, ден. ед.	Количество, шт.
	товара X	товара Y
40	4	14
35	5	10
34		8
	7	6
30	8

Задания повышенной сложности

1. Постройте кривые безразличия нетипичной формы и определите значение предельной нормы замещения в каждом случае. Приведите примеры товаров для различных форм кривых безразличия.

2. Изучите алгоритм построения кривых «цена – потребление» и «доход – потребление». На основе кривой «цена – потребление» постройте линию спроса для одного из товаров.

рекомендуемая литература

[4, с. 193 – 206]; [6, с. 120 – 157]; [7, с. 72 – 123]