Задача линейного программирования может быть задана в общей форме записи, симметричной (или стандартной) и канонической.

Возьмем задачу линейного программирования, заданную в общей форме записи: максимизировать функцию:

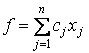             (2.1)

при ограничениях

        (2.2)

                (2.3)

.                (2.4)

Если в задаче линейного программирования требуется максимизировать целевую функцию (2.1) при ограничениях (2.2), (2.4), то задача задана в симметричной форме записи.

Задача линейного программирования, в которой требуется найти максимум функции (2.1) при ограничениях (2.3) и (2.4), задана в канонической форме записи.

При использовании тех или иных методов решения задач линейного программирования приходится осуществлять переходы от одной формы записи задачи к другой. Задача минимизации может быть сведена к задаче максимизации и наоборот, если в качестве критерия эффективности новой задачи взять критерий эффективности исходной задачи со знаком минус.

Так, задача минимизации  эквивалентна задаче максимизации . Если при этом минимальное значение критерия эффективности в исходной задаче равно , то в новой задаче максимальное значение критерия равно  , а оптимальные стратегии в обеих задачах совпадают. Каждое ограничение (2.2) типа меньше или равно можно заменить на ограничение типа больше или равно путем умножения на  –1.

Каждое ограничение типа неравенства можно заменить на ограничение типа равенства, вводя новую неотрицательную переменную, называемую свободной. Так любое ограничение

 можно записать в виде:

,

а ограничение  записывается в виде:

.

Ограничение типа равенства  эквивалентно двум ограничениям:

.

Если в задаче имеется переменная не подчиненная условию неотрицательности (2.4), то ее можно заменить на две неотрицательные переменные, применяя преобразование вида . Если переменная  ограничена снизу не нулем, а некоторой константой . То заменой переменных  можно перейти к неотрицательной переменной .

Пример 1

Привести к канонической форме записи задачу:

.

Решение

Заменяем функцию  на функцию . Путем вычитания свободной неотрицательной переменной  из левой части первого неравенства приводим его к уравнению. Второе ограничение-неравенство приводим к уравнению путем прибавления к его левой части свободной неотрицательной переменной . Произвольную переменную  заменяем разностью  неотрицательных переменных  и . Таким образом, задача в канонической форме записи имеет вид:

.