Совокупность действий, связанных с составлением уравнения регрессии, называется регрессионным анализом. Регрессионный анализ результатов однофакторного эксперимента включает в себя следующие действия:
1) подбор вида уравнения регрессии. Осуществляется с помощью, например, функциональных шкал;
2) определение постоянных коэффициентов в уравнении регрессии. Осуществляется с помощью МНК;
3) проверку соответствия (адекватности) уравнения регрессии результатам опытов.
Проверка адекватности уравнения регрессии результатам опытов проводится следующим образом:
1) По результатам повторных изменений в каждом опыте вычисляются дисперсия функции отклика (σу2), среднеквадратичная погрешность (![]() ), доверительный интервал 9
), доверительный интервал 9![]() ), математическое ожидание (
), математическое ожидание (![]() ).
).
2) Осуществляется проверка однородности дисперсии ![]() , где j = 1,2,…, N – число опытов. Дисперсии
, где j = 1,2,…, N – число опытов. Дисперсии ![]() называются однородными, если при неограниченном увеличении числа повторных измерений п в каждом из опытов они стремятся к общему пределу, т.е.
называются однородными, если при неограниченном увеличении числа повторных измерений п в каждом из опытов они стремятся к общему пределу, т.е.
![]() .
.
Дисперсии проверяются на однородность с помощью критериев Фишера, Кохрена, Бартлета. Наиболее просто осуществить проверку однородности с помощью критерия Фишера. Для этого из всех дисперсий (![]() ) выбирают две: наибольшую (
) выбирают две: наибольшую (![]() ) и наименьшую (
) и наименьшую (![]() ).
).
Отношение ![]() /
/![]() сравнивают с табличным значением критерия Фишера (F):
сравнивают с табличным значением критерия Фишера (F):
· если ![]() /
/![]() < F – дисперсии
< F – дисперсии ![]() и
и ![]() однородны, следовательно, однородны и все дисперсии, лежащие в промежутке
однородны, следовательно, однородны и все дисперсии, лежащие в промежутке ![]() <
<![]() <
<![]() ;
;
· если ![]() /
/![]() > F – дисперсии неоднородны.
> F – дисперсии неоднородны.
Значения критерия Фишера берутся из таблицы 2.3, составленной при доверительной вероятности Р = 0,95, для числа степеней свободы числителя (дисперсии ![]() ) и числа степеней свободы знаменателя (дисперсии
) и числа степеней свободы знаменателя (дисперсии ![]() ).
).
Таблица 2.3
|
fзнам |
fчисл |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
12 |
24 |
∞ |
|
|
1 2 3 4 5 6 7 8 9 10 12 24 ∞ |
164,4 18,5 10,1 7,7 6,6 6,0 5,6 5,3 5,1 5,0 4,8 4,3 3,8 |
199,5 19,2 9,6 6,9 5,8 5,1 4,7 4,5 4,3 4,7 3,9 3,4 3,0 |
215,7 19,2 9,3 6,6 5,4 4,8 4,4 4,1 3,9 3,7 3,5 3,0 2,6 |
224,6 19,3 9,1 6,4 5,2 4,5 4,1 3,8 3,6 3,5 3,3 2,8 2,4 |
230,2 19,3 9,0 6,3 5,1 4,4 4,0 3,7 3,5 3,3 3,1 2,6 2,2 |
234,9 19,3 8,9 6,2 5,0 4,3 3,9 3,6 3,4 3,2 3,0 2,5 2,1 |
244,9 19,4 8,7 5,9 4,7 4,0 3,6 3,3 3,1 2,9 2,7 2,2 1,8 |
249,0 19,5 8,6 5,8 4,5 3,8 3,4 3,1 2,9 2,7 2,5 2,0 1,5 |
254,3 19,5 8,5 5,6 4,4 3,7 3,2 2,9 2,7 2,5 2,3 1,7 1,0 |
Если в каждом из опытов число повторных измерений одинаково и равно п, то fчисл = fзнам = п – 1. Если дисперсии ![]() и
и ![]() неоднородны, то это означает, что число повторных измерений недостаточно или что среди результатов повторных измерений опыта с дисперсией
неоднородны, то это означает, что число повторных измерений недостаточно или что среди результатов повторных измерений опыта с дисперсией ![]() находится промах.
находится промах.
Следует очистить результаты повторных измерений от промахов, увеличить число повторных измерений, снова определить ![]() и проверить их однородность. Если все дисперсии
и проверить их однородность. Если все дисперсии ![]() и
и ![]() однородны, можно переходить к следующему действию.
однородны, можно переходить к следующему действию.
3) Вычисляется дисперсия воспроизводимости (S2воспр). Дисперсия воспроизводимости – это среднее из дисперсий (![]() ) всех опытов. Дисперсия воспроизводимости характеризует средний разброс результатов повторных измерений во всех опытах относительно своих математических ожиданий.
) всех опытов. Дисперсия воспроизводимости характеризует средний разброс результатов повторных измерений во всех опытах относительно своих математических ожиданий.
Если в каждом опыте число повторных измерений одинаково и равно п, то S2воспр определяется по формуле:
S2воспр = 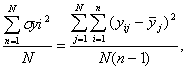
где N – число опытов, ![]() – математическое ожидание в j-м опыте. Если в опытах число повторных измерений различно, то S2воспр определяется как средневзвешенная величина
– математическое ожидание в j-м опыте. Если в опытах число повторных измерений различно, то S2воспр определяется как средневзвешенная величина
S2воспр = 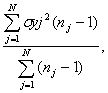
где ![]() - число повторных измерений в j-м опыте.
- число повторных измерений в j-м опыте.
Число степеней свободы дисперсии воспроизводимости равно сумме чисел степеней свободы дисперсий опытов:
![]() .
.
4) Вычисляется дисперсия адекватности (S2ад). Дисперсия адекватности – это сумма квадратов отклонений расчётных и экспериментальных значений функции отклика в каждом опыте, отнесённая к числу степеней свободы. Она характеризует разброс экспериментальных результатов относительно расчётных и определяется по формуле:
S2ад = 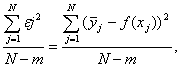
где т – число постоянных коэффициентов в уравнении регрессии; ![]() — математическое ожидание в j-м опыте; N – m = fад – число степеней свободы дисперсии адекватности;
— математическое ожидание в j-м опыте; N – m = fад – число степеней свободы дисперсии адекватности;
3) Проверяется однородность дисперсий адекватности и воспроизводимости. Дисперсии адекватности и воспроизводимости будут однородными, если их отношение будет меньше табличного значения критерия Фишера:
S2ад / S2воспр < F,
где значения F берутся (см. табл. 2.3)для числа степеней свободы числителя (дисперсии адекватности) и числа степеней свободы знаменателя (дисперсия воспроизводимости).
Если дисперсии S2ад и S2воспр однородны ![]() , то с доверительной вероятностью Р = 0,95 можно утверждать, что составленное уравнение регрессии адекватно. Это следует из того, что при
, то с доверительной вероятностью Р = 0,95 можно утверждать, что составленное уравнение регрессии адекватно. Это следует из того, что при ![]() и
и ![]() разброс экспериментальных значений функции отклика относительно её расчётных значений равен среднему разбросу результатов повторных измерений в каждом опыте относительно своих математических ожиданий.
разброс экспериментальных значений функции отклика относительно её расчётных значений равен среднему разбросу результатов повторных измерений в каждом опыте относительно своих математических ожиданий.
Если S2ад / S2воспр > F, то выбранное уравнение регрессии неадекватно. Следует перейти к уравнению регрессии более высокого порядка или выбрать уравнение регрессии другого вида, определить значения коэффициента и снова проверить адекватность.
Если опыты состоят из однократных измерений, то адекватность уравнения регрессии не может быть проверена изложенным способом. В этом случае проверка адекватности уравнения регрессии может быть осуществлена сравнением доверительного интервала функции отклика (ау) с отклонениями расчётных и экспериментальных значений функции отклика (![]() ). Очевидно, что, если
). Очевидно, что, если ![]() < ау, то уравнение регрессии адекватно.
< ау, то уравнение регрессии адекватно.