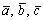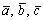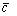Пусть — три произвольных вектора.Три вектора называются компланарными , если они параллельны одной плоскости, т.е., будучи приведены к одному началу, лежат в одной плоскости. Смешанным произведением векторов называется число равное скалярному произведению векторного произведения векторов на вектор т.е. Геометрический смысл смешанного произведения определяется следующей теоремой. Теорема 2.1. Смешанное произведение равно объему параллелепипеда V , построенного на векторах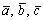, взятому со знаком «+», если тройка векторов 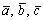правая, и со знаком «- «, если тройка векторов 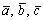левая. Если векторы 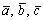компланарны, то смешанное произведение рано нулю, т.е.