2.1. Через блок, укрепленный на конце стола, перекинута нерастяжимая нить, к концам которой прикреплены грузы (рис. 2.2). Один груз массой m₁ = 400 г движется по поверхности стола, а другой массой m₂ = 600 г движется вдоль вертикали вниз. Коэффициент трения груза о стол равен: f = 0,1. Считать нить и блок невесомыми. Определить: 1) ускорение (), с которым движутся грузы; 2) силу натяжения (T) нити.

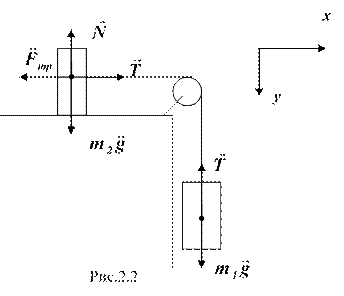Дано:     m₁ = 400 г = 0,4 кг,   m₂ = 600 г = 0,6 кг, f = 0,1.

Определить: , T.

Решение: Выбрав оси координат, запишем для каждого груза уравнение движения (второй закон Ньютона) в проекциях на оси:

; .

Учитывая, что , получим систему уравнений:

,

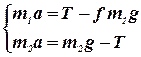откуда искомое ускорение:

.

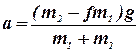Силу натяжения нити найдем из второго уравнения системы:

.

Вычисляя, получим:

; .

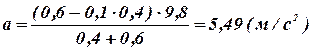Проверка размерности:

; .

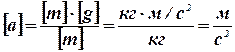1)  = 5,49 м/с²; 2) Т = 2,59 Н.

2.2. Снаряд массой  m₁ = 100 кг, летящий горизонтально со скоростью 500 м/с, попадает в вагон с песком массой m₂ = 10 т и застревает в нем.

Какую скорость () получит вагон, если он двигался со скоростью 36 км/ч в направлении, противоположном движению снаряда?

Дано:   = 500 м/с;     = 36 км/ч = 10 м/с;

            m₁ = 100 кг;      m₂ = 10 т = 10⁴ кг

Определить: 

Решение: Запишем для снаряда и вагона с песком уравнение закона сохранения импульса:

Выбирая направление оси  совпадающим с направлением движения снаряда и проецируя на неё обе части предыдущего уравнения, получим:

,

откуда 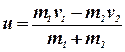 ,                  (м/с)

Проверка размерности:  .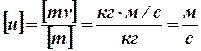

Следовательно, вагон со снарядом будет двигаться в отрицательном направлении оси .