Пусть на плоскости задана прямоугольная система координат: 0 — начало координат,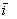 , 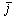— единичные направляющие векторы осей координат. Рассмотрим на плоскости 0 ху произвольную прямую l .Уравнением прямой l называется уравнение, содержащее переменные х , у , которому удовлетворяют координаты любой точки, лежащей на l , и не удовлетворяют координаты никакой точки, не лежащей на l . Прямая однозначно определяется:1) точкой и вектором, перпендикулярным l (нормальным вектором);2) точкой и вектором, параллельным (направляющим вектором);3) ее двумя точками;4) угловым коэффициентом и начальной ординатой.В каждом из этих случаев получим соответствующий вид уравнения прямой. 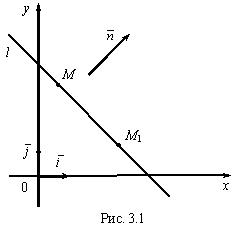Пусть прямая l (рис. 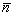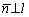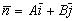3.1) определена точкой M 1 ( x 1 , y 1 ), лежащей на l , и нормальным вектором (т.е.);, (или, что то же самое, 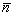={ A , B }). Пусть М ( х , у ) — любая точка прямой. Тогда вектор 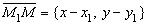перпендикулярен вектору, поэтому скалярное произведение этих векторов равно нулю (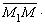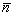= 0). Выражая это произведение через координаты сомножителей, получим:

, (3.1)

т.е. уравнение прямой, проходящей через данную точку М ( х 1, у 1) перпендикулярно данному вектору 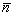= { A , B }.

Преобразуем уравнение (3.1). Раскрыв скобки и переставив слагаемые, получим:

.

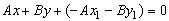
Обозначим число (- Ах 1 — By 1) через С и получим:

(3.2)

- общее уравнение прямой.

Итак, уравнение прямой (3.1) является уравнением первой степени относительно переменных х , у (координат произвольной точки М , которые называются текущими координатами).Покажем, что любое уравнение первой степени (3.2) есть уравнение некоторой прямой на плоскости 0 ху . Для этого приведем уравнение (3.2) к виду (3.1).Если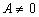 , то уравнение (3.2) равносильно уравнению:

.

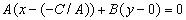
Если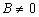, то уравнение (3.2) равносильно уравнению:

.

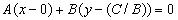
В любом случае получаем уравнение прямой, проходящей через некоторую точку, перпендикулярно известному вектору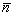={ A , B }.

Итак, уравнение (3.2) является уравнением некоторой прямой. Его коэффициенты А , В являются координатами нормального вектора.Если в уравнении (3.2) С = 0, то прямая l проходит через начало координат. Если А = 0 (,), т.е. уравнение имеет вид у = у 1, (), то прямая l параллельна оси 0 х . Если В = 0 (,), т.е. уравнение имеет вид , (), то прямая l параллельна оси 0 у . Уравнение у = 0 ( А = С = 0) является уравнением оси 0 х , а уравнение ( В = С = 0) — уравнением оси 0 y . Пусть прямая l (рис. 3.2) задана своей точкой M 1 ( x 1 , y 1 ) и направляющим вектором . Тогда векторы коллинеарны, следовательно, их соответствующие координаты пропорциональны, т.е.

. (3.3)

Полученное уравнение является уравнением искомой прямой l и называется каноническим . Может оказаться, что вектор перпендикулярен одной из осей, тогда, либо m = 0, либо n = 0. В этих случаях каноническое уравнение прямой все равно будем записывать соответственно в виде:

.

Пусть прямая l проходит через две заданных точки M 1 ( x 1 , y 1 ) и M 2 ( x 2 , y 2 ) (рис. 3.3). Тогда векторы и коллинеарны, поэтому уравнение

(3.4)

является уравнением прямой, проходящей через точки М 1 ( х 1 , у 1 ) и М 2 ( х 2 , у 2 ).

Пусть прямая l пересекает оси координат в точках М 1(0, b ), М 2( a , 0) (рис. 3.4). Запишем уравнение прямой l в виде (3.4), отсюда получаем:

. (3.5)

Уравнение (3.5) называется уравнением прямой в отрезках ( а и b — отрезки, отсекаемые прямой l на осях координат).Пусть прямая l образует с осью 0 х угол (рис. 3.5) и проходит через точку М 1 ( х 1 , у 1 ). Запишем каноническое уравнение прямой l , взяв в качестве направляющего вектора вектор = { m , n } единичной длины, который составляет с осью 0 х угол . Очевидно, что т = cos, n = sin и уравнение прямой l принимает вид:

Если (т.е. l неперпендикулярна оси 0 х ), то из последнего уравнения получаем:

.

Пусть k = tg (это число называется угловым коэффициентом прямой), тогда можно записать

(3.6)

уравнение прямой с угловым коэффициентом k, проходящей через данную точку М 1 (х 1 , у 1 ) .

Если в качестве точки М 1 взять точку М 0 (0, b ) пересечение прямой l с осью 0у (рис. 3.6), то уравнение (3.6) примет вид:

. (3.7)

Полученное уравнение называется уравнением прямой с угловым коэффициентом k и начальной ординатой b . Пример 3.1. Записать всевозможные уравнения прямой, проходящей через точки М 1 (2, — 3) и М 2 (1, 0) (рис. 3.7). Решение. Используя уравнение (3.4), получим уравнение прямой, проходящей через точки М 1 и М 2 :, отсюда получаем:

- каноническое уравнение прямой. Сделав очевидные преобразования, получим:

- уравнение прямой l , проходящей через точку М 1(2, — 3) перпендикулярно вектору = {3, 1}. После раскрытия скобок и приведения подобных слагаемых получим общее уравнение прямой: . Наконец, выразив отсюда у , получим — уравнение с угловым коэффициентом и начальной ординатой.

Пример 3.2. Дано общее уравнение прямой l :. Найти отрезок, отсекаемый этой прямой от оси 0 у и угол между l и осью 0 х . Построить прямую l . Решение. Решим данное уравнение относительно переменной у , получим:

- уравнение прямой l с угловым коэффициентом k = tg = — 1 и начальной ординатой b = 10/3. Значит, прямая l проходит через точку М 1 (0, 10/3) и составляет с осью 0 х угол =. По этим данным строим прямую l (рис. 3.8).