Мы рассмотрели четыре вида кривых второго порядка: окружность, эллипс, гиперболу и параболу. Рассматривая общее уравнение второго порядка:

при отсутствии члена Вху (исследовали случай при В = 0), мы видели, что данное уравнение при различных соотношениях между коэффициентами А , С , D , Е может описывать либо одну из перечисленных четырех кривых, либо точку, либо пару пересекающихся прямых, либо не определять ничего. Кроме перечисленных случаев, уравнение (3.17) может определять еще две параллельные прямые или одну прямую (например, уравнение 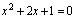задает прямую).

Пусть теперь уравнение (3.17) содержит член с произведением ху (т.е. В 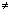0). Покажем, что можно, осуществляя поворот системы координат, перейти к новым координатам так, что уравнение (3.17) в новых координатах не будет содержать члена с произведением координат ху .Если новая система 0 XY получается из старой 0 ху поворотом на угол 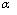, то переход от старых координат к новым происходит по формулам:

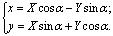
(3.22)

При подстановке х , у по формулам (3.22) в уравнение (3.17) слагаемые Dx и Еу дадут лишь первые степени Х и Y . Поэтому преобразуем сумму: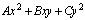

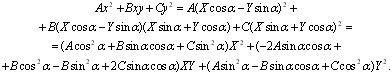
Преобразуем коэффициент при XY :

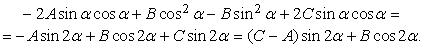
Выберем угол поворота 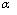так, чтобы этот коэффициент был равен нулю:

.

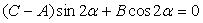
Это всегда возможно. Действительно, при С = А будет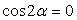, следовательно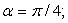, при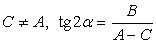, следовательно,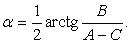

Итак, с помощью поворота системы координат получили, что в новых координатах уравнение (3.17) не содержит члена с произведением координат ху . Выделяя далее полные квадраты, приведем уравнение к каноническому виду.Известно, что уравнение (3.17) может описывать только перечисленные ранее линии.