Пусть в пространстве задана прямоугольная декартова система координат 0 xyz . Поверхность называется поверхностью второго порядка , если она задается уравнением второй степени относительно текущих координат х , у , z . Сферой называется множество точек в пространстве, удаленных от данной точки (называемой центром) на одно и то же расстояние (называемое радиусом).Выведем уравнение сферы. Пусть S ( a , b , с ) — центр сферы, R — радиус сферы, М ( х , у , z ) — произвольная точка сферы. По определению сферы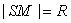. Так как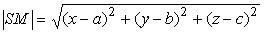, то получаем: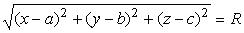. Возведя обе части этого уравнения в квадрат, имеем:

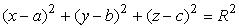
- уравнение сферы с центром в точке S ( a , b , c ) и радиусом R . Если центр совпадает с началом координат 0(0, 0, 0), то получаем

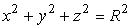
- каноническое уравнение сферы.

Цилиндрической поверхностью называется множество всех прямых, пересекающих данную линию L и параллельных данной прямой l . Линия L называется направляющей для цилиндрической поверхности, а прямые, составляющие ее (параллельные прямой l ), называются ее образующими (рис. 3.28).

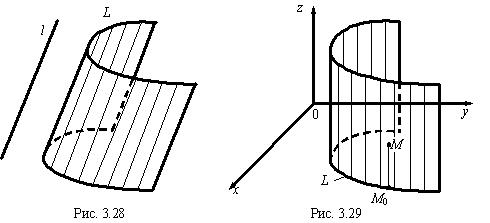
Зададим в пространстве систему координат 0 хуz , направляющую линию L будем располагать в одной из координатных плоскостей (например, в плоскости 0 ху ), а образующие направим параллельно оси координат, которая перпендикулярна этой плоскости (ось 0 z ).Пусть в плоскости 0 ху задана линия L с уравнением F ( x , y ) = 0 (рис. 3.29). Построим цилиндрическую поверхность с направляющей L и образующими, параллельными 0 z . Покажем, что эта цилиндрическая поверхность задается тем же уравнением F ( x , y ) = 0, что и направляющая линия L , если точки рассматривать в пространстве.Пусть М ( x , у , z ) — произвольная точка цилиндрической поверхности, а М 0 — ее проекция на плоскость 0 ху , она является точкой пересечения L и образующей, проходящей через М , поэтому точки М и М 0 имеют одну и ту же абсциссу х , одну и ту же ординату у . Поскольку М 0 лежит на линии L , то ее координаты х , у удовлетворяют уравнению F ( x , у ) = 0, поэтому и координаты точки М ( х , у , z ) также удовлетворяют этому уравнению (ведь z в нем не встречается). Координаты всякой точки, не лежащей на данной цилиндрической поверхности, не будут удовлетворять уравнению F ( x , у ) = 0, так как эти точки не будут проецироваться на линию L .Итак, данная цилиндрическая поверхность в пространстве задается уравнением: F ( x , у ) = 0 (как и ее направляющая L в плоскости 0 ху ).В пространстве 0 xyz линия L будет задаваться системой уравнений:

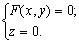
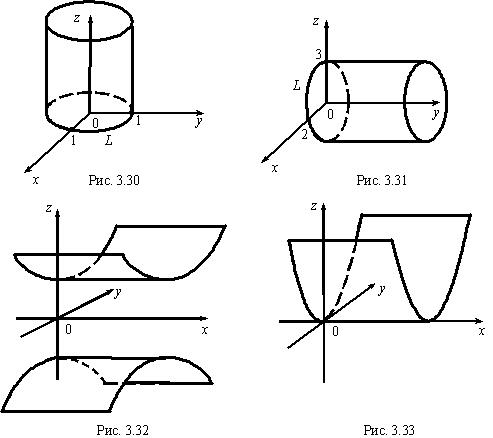
Нас интересуют цилиндрические поверхности второго порядка, следовательно, их направляющими будут: окружность, эллипс, гипербола, парабола. Сами поверхности будут называться соответственно: круговым цилиндром, эллиптическим цилиндром, гиперболическим цилиндром и параболическим цилиндром.Примеры цилиндрических поверхностей:1) Направляющая L в плоскости 0 ху имеет уравнение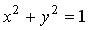, т.е. является окружностью, образующие параллельны 0 z . Имеем круговой цилиндр (рис. 3.30).2) Направляющая линия L — эллипс в плоскости 0 xz с уравнением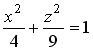, образующие параллельны оси 0 у . Имеем эллиптический цилиндр (рис. 3.31).3) Гиперболический цилиндр, заданный уравнением, имеет направляющей линией гиперболу в плоскости 0 yz с действительной полуосью 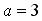и мнимой полуосью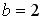. Образующие параллельны оси 0 х (рис. 3.32).4) Для параболического цилиндра (рис. 3.33) направляющей линией является парабола: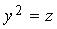, лежащая в плоскости 0 yz , его образующие параллельны оси 0 х .