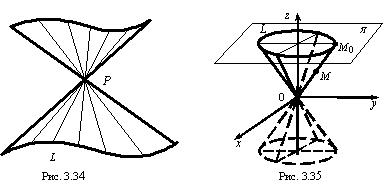
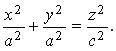Конической поверхностью называется множество прямых, проходящих через данную точку Р и пересекающих данную линию L . Точка Р называется вершиной, линия L — направляющей, а прямые — образующими конической поверхности (рис. 3.34).

Рассмотрим коническую поверхность второго порядка, у которой вершиной будет служить начало координат 0(0, 0, 0), а в качестве направляющей L будет эллипс, расположенный в плоскости , параллельной плоскости 0 ху и отстоящей от нее на расстоянии с (рис. 3.35). Такой эллипс задается системой:

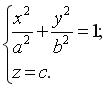
(3.23)

Выведем уравнение этой конической поверхности. Пусть М ( х , у, z ) — произвольная точка поверхности, М 0( х 0, у 0, z 0) — точка пересечения эллипса с образующей ОМ . Координаты точки М 0 удовлетворяют системе (3.23), поэтому

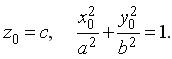
(3.24)

link rel=»stylesheet» href=»styles.css»>

Запишем уравнения прямой ОМ 0: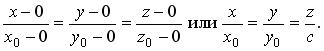 Выразим из этих уравнений х 0 и у 0: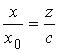, отсюда 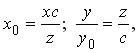получаем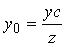. Подставим найденные значения х 0, у 0 в равенство (3.24):

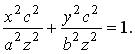
Умножим последнее равенство на: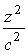

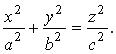
(3.25)

Уравнение (3.25) является уравнением конуса второго порядка. В частности, если a=b , то имеем круговой конус, который задается уравнением: