Эллиптическим параболоидом называется поверхность, определяемая в некоторой декартовой системе координат уравнением:

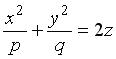
, (3.37)

где р и q одного знака.

Пусть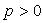, , 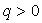тогда z 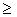0, причем z = 0 при х = 0 и у = 0. Следовательно, с плоскостью 0 ху эта поверхность имеет единственную общую точку 0(0, 0, 0). Рассмотрим сечение параболоида плоскостью 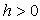z = h , (эта плоскость параллельна плоскости 0 ху ):

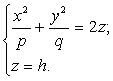
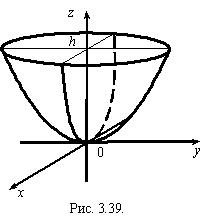
Видим, что сечение — эллипс с полуосями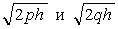. Сечения с плоскостями 0 ху и 0 уz являются параболами:

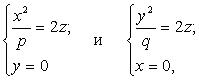
причем 0 z является их общей осью (рис. 3.39). Oсь 0 z является осью параболоида (3.37). Если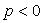, ,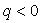 то параболоид будет располагаться ниже плоскости 0 ху .

Гиперболическим параболоидом называется поверхность, уравнение которой имеет вид:

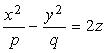
, (3.38)

где р и q одинакового знака.

Пусть,. Рассмотрим сечения этой поверхности плоскостями 0 xz и 0 yz , получим, соответственно, параболы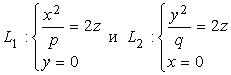, причем ветви первой направлены вверх, а ветви второй — вниз (рис. 3.40). С плоскостью 0 ху параболоид

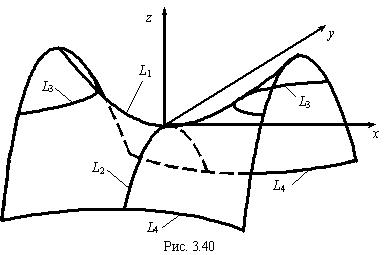
имеет сечение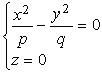, что равносильно двум системам:

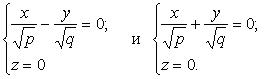
(3.39)

Системы (3.39) задают в плоскости 0 ху две прямые, проходящие через начало координат.Пусть плоскость параллельна 0 ху и удалена от нее на h (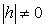), тогда в пересечении с параболоидом (3.38) получится гипербола

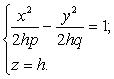
(3.40)

При 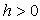гипербола (3.40) имеет действительную полуось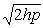, мнимую полуось 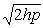(рис. 3.40, L 3). При 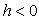гипербола (3.40) имеет действительную полуось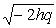, а мнимую — 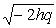(рис. 3.40, L 4).