Пусть линия L лежит в плоскости 0 ху и задается в пространстве системой
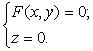
Рассмотрим поверхность, образованную вращением линии L вокруг оси 0 у (рис. 3.41), и выведем уравнение этой поверхности.Пусть
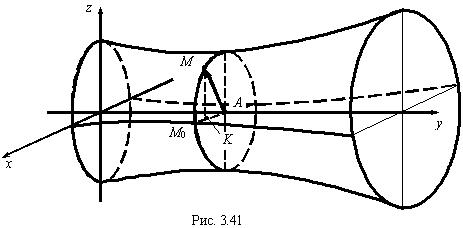
AM = AM 0 = x 0 , z 0 = 0 , y 0 = y и F ( x 0 , y 0) = 0 . (3.41)
Из 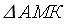 имеем:
имеем: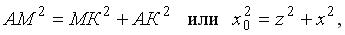 отсюда
отсюда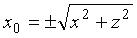 . Учитывая, что у 0 = у , из равенств (3.41) получаем:
. Учитывая, что у 0 = у , из равенств (3.41) получаем:
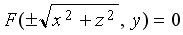
, (3.42)
т.е. координаты любой точки поверхности вращения удовлетворяют уравнению (3.42). Следовательно, это уравнение является уравнением данной поверхности вращения.
Если линия L лежит в плоскости 0 уz и определяется системой
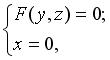
то поверхность, образованная вращением L вокруг оси 0 z , задается уравнением: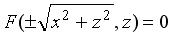 . Если L вращается вокруг оси 0 у , то поверхность вращения будет иметь уравнение:
. Если L вращается вокруг оси 0 у , то поверхность вращения будет иметь уравнение: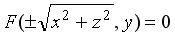 . Аналогично в случае, когда L вращается вокруг оси 0 x .
. Аналогично в случае, когда L вращается вокруг оси 0 x .
Пример 3.11. Найти уравнение и определить вид поверхности, образованной вращением эллипса 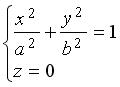 вокруг оси 0 у . Решение. Заменяя в уравнении
вокруг оси 0 у . Решение. Заменяя в уравнении 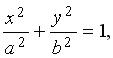 x 2 на x 2 + z 2, получим уравнение эллипсоида:
x 2 на x 2 + z 2, получим уравнение эллипсоида: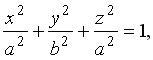 называемого эллипсоидом вращения. Пример 3.12. Парабола
называемого эллипсоидом вращения. Пример 3.12. Парабола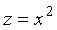 , лежащая в плоскости у = 0 вращается вокруг оси 0 z . Определить вид получаемой поверхности и записать ее уравнение. Решение. Заменим х 2 в уравнении z = х 2 на х 2 + у 2, получаем уравнение эллиптического параболоида:
, лежащая в плоскости у = 0 вращается вокруг оси 0 z . Определить вид получаемой поверхности и записать ее уравнение. Решение. Заменим х 2 в уравнении z = х 2 на х 2 + у 2, получаем уравнение эллиптического параболоида: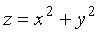 , называемого параболоидом вращении.
, называемого параболоидом вращении.
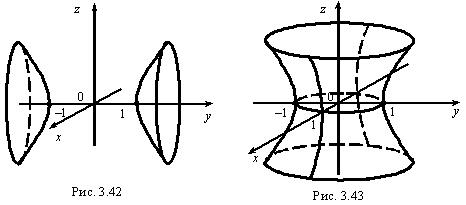
Пример 3.13. Какие поверхности образует гипербола
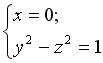
(3.43)
при вращении вокруг осей 0 у и 0 z ?
Решение. При вращении гиперболы (3.43) вокруг оси 0 у получаем: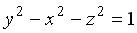 — двуполостный гиперболоид (рис. 3.42), а при вращении ее вокруг оси 0 z получаем однополостный гиперболоид
— двуполостный гиперболоид (рис. 3.42), а при вращении ее вокруг оси 0 z получаем однополостный гиперболоид 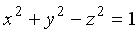 (рис. 3.43).
(рис. 3.43).