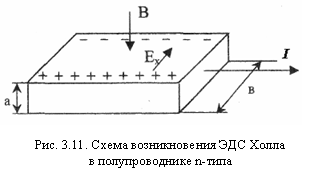
 Если полупроводник, вдоль которого течет электрический ток (рис. 3.11), поместить в магнитное поле, перпендикулярно направлению тока, то в полупроводнике возникнет поперечное электрическое поле, перпендикулярное току и магнитному полю. Это явление получило название эффекта Холла, а возникающая при этом поперечная ЭДС получило название ЭДС Холла.
Если полупроводник, вдоль которого течет электрический ток (рис. 3.11), поместить в магнитное поле, перпендикулярно направлению тока, то в полупроводнике возникнет поперечное электрическое поле, перпендикулярное току и магнитному полю. Это явление получило название эффекта Холла, а возникающая при этом поперечная ЭДС получило название ЭДС Холла.
Движущиеся электроны, создающие ток (I) вдоль полупроводника будут отклоняться силой Лоренца в соответствии с правилом левой руки к задней грани полупроводника. У передней грани останутся нескомпенсированные ионы донорной примеси. Благодаря такому разделению зарядов появится поперечное электрическое поле, которое будет препятствовать дальнейшему отклонению электронов к задней грани пластины. Состояние равновесия установится при равенстве силы, действующей на электроны со стороны поперечного поля, силе Лоренца.
Электродвижущая сила Холла (в вольтах), т.е. разность потенциалов, соответствующая равновесному состоянию, находится из выражения:
Ux = R![]() , (3.27)
, (3.27)
где R – коэффициент Холла; I – ток, протекающий по полупроводнику; В – магнитная индукция; d – толщина пластины.
В соответствии с рис. 3.11 поперечная разность потенциалов может быть найдена из выражения:
Ux = вEx, (3.28)
где в – ширина пластины; Еx, – напряженность поперечного электрического поля.
Сила Лоренца, действующая на электрон, находится из выражения:
F = evB, (3.29)
где е – заряд электрона; v – скорость электрона; В – магнитная индукция.
При равновесии еЕx = -еvB получим:
Ex = -vB,
тогда
Ux= -evB. (3.30)
Произвольный ток в полупроводнике может быть найден из выражения:
I = nevвd. (3.31)
Из выражения (3.31) получим:
вv = I/(n ed).
Тогда выражение (3.30) примет вид:
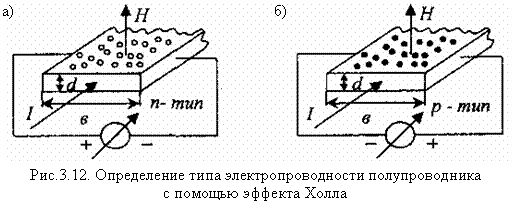 Ux = – I B / (n ed). (3.32)
Ux = – I B / (n ed). (3.32)
Сравнивая выражения (3.32) и (3.27), получим:
для электронного полупроводника:
R = -1/( en), (3.33)
аналогично для дырочного полупроводника
R = 1/(ep). (3.34)
Выражения (3.33) и (3.34) получены без учёта рассеивания свободных носителей заряда на тепловых колебаниях решетки. С учётом этого рассеяния:
для электронного полупроводника
R ≈ -1,17 / ( en), (3.35)
для дырочного полупроводника
R ≈ 1,17/( en), (3.36)
С учетом рассеяния на ионах примеси для электронного полупроводника
R ≈ -1,13/( en), (3.37)
для дырочного полупроводника
R≈1,17/( en). (3.38)
Если полупроводник обладает электропроводностью смешанного типа, то
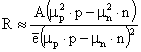 , (3.39)
, (3.39)
где А – коэффициент рассеяния (при рассеянии на тепловых колебаниях А ≈ 1,17, на ионах примесей А ≈ 1,93; μp и μn – подвижности дырок и электронов соответственно.
Для собственного полупроводника R отличен от нуля ввиду неравенства подвижностей электронов и дырок, концентрации которых равны (n = р = n). В этом случае R определяется из выражения:
![]() . (3.40)
. (3.40)
С помощью эффекта Холла можно определить тип электропроводности полупроводника следующим образом (рис. 3.12).