Пусть даны две прямые l 1 и l 2 на плоскости:
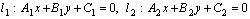
.
Чтобы определить их взаимное расположение, достаточно решить систему уравнений:
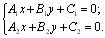
(3.8)
Если эта система имеет единственное решение ( х 0, у 0), то прямые l 1 и l 2, пересекается в точке М 0( х 0, у 0). Если система (3.8) не имеет решений, то прямые l 1 и l 2 не пересекаются, следовательно, l 1 || l 2. Если система (3.8) имеет бесконечное множество решений, то l 1 и l 2 совпадают.Однако решить вопрос о взаимном расположении l 1 и l 2 можно и не решая системы (3.3). Действительно, из общего уравнения прямой l 1, находим, что ее нормальный вектор 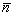 имеет координаты А 1 и В 1 , т.е.
имеет координаты А 1 и В 1 , т.е.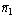 = { А 1, В 1}, а прямая l 2 имеет нормальный вектор
= { А 1, В 1}, а прямая l 2 имеет нормальный вектор 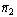 = { А 2, В 2}. Если векторы
= { А 2, В 2}. Если векторы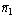 ,
,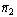 коллинеарны, то прямые l 1 и l 2 либо параллельны, либо совпадают. Если
коллинеарны, то прямые l 1 и l 2 либо параллельны, либо совпадают. Если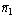 ,
,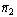 неколлинеарны, то прямые пересекаются. Зная, что коллинеарные векторы (и только они) имеют пропорциональные координаты, получаем: если
неколлинеарны, то прямые пересекаются. Зная, что коллинеарные векторы (и только они) имеют пропорциональные координаты, получаем: если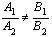 , то прямые l 1 и l 2 пересекаются; если
, то прямые l 1 и l 2 пересекаются; если 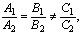 ,то прямые l 1 и l 2 параллельны; если
,то прямые l 1 и l 2 параллельны; если 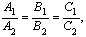 ,то прямые l 1 и l 2 совпадают.
,то прямые l 1 и l 2 совпадают.
Используя нормальные векторы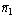 ,
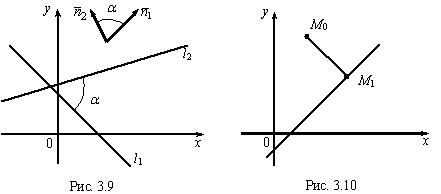
,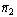 можно также найти угол между прямыми, так как угол между нормальными векторами равен одному из углов между прямыми l 1 и l 2 (рис. 3.9).
можно также найти угол между прямыми, так как угол между нормальными векторами равен одному из углов между прямыми l 1 и l 2 (рис. 3.9).
Из определения скалярного произведения векторов получаем: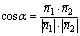 , поэтому
, поэтому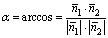 .Пусть на плоскости заданы прямая
.Пусть на плоскости заданы прямая 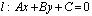 и точка М 0( х 0, у 0). Найдем расстояние d от точки М 0( х 0, у 0) до прямой l (рис. 3.10). Пусть М 1( х 1, у 1) — точка пересечения прямой l и прямой, проходящей через точку М 0 перпендикулярно l . Так как М 1 лежит на l , то ее координаты удовлетворяют уравнению этой прямой, таким образом, имеем тождество:
и точка М 0( х 0, у 0). Найдем расстояние d от точки М 0( х 0, у 0) до прямой l (рис. 3.10). Пусть М 1( х 1, у 1) — точка пересечения прямой l и прямой, проходящей через точку М 0 перпендикулярно l . Так как М 1 лежит на l , то ее координаты удовлетворяют уравнению этой прямой, таким образом, имеем тождество:
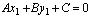
. (3.9)
Рассмотрим вектор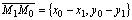 . Этот вектор коллинеарен нормальному вектору
. Этот вектор коллинеарен нормальному вектору 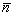 = { А 1, В 1} прямой l и
= { А 1, В 1} прямой l и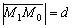 , поэтому косинус угла между векторами
, поэтому косинус угла между векторами 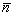 и
и  равен либо 1, либо -1. Следовательно,
равен либо 1, либо -1. Следовательно,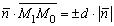 , откуда
, откуда
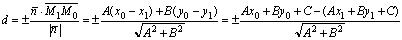
.
Учитывая тождество (3.9) получаем:
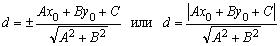
. (3.10)
Пример 3.3. Найти расстояние от точки пересечения прямых l l и l 2 до прямой l 3. Определить взаимное расположение пар прямых l 1, l 3 и l 2, l 3, если прямые заданы общими уравнениями:
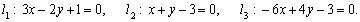
Решение. Решим систему уравнений:
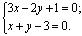
Получим: х 0 = 1, у 0 = 2 — единственное решение. Следовательно, прямые l 1 и l 2 пересекается в точке М 0(1, 2). Используя формулу (3.10), найдем расстояние d от М 0 до l 3:
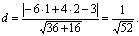
Нормальные векторы прямых l 1, l 2 и l 3 соответственно будут 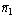 = {3, — 2},
= {3, — 2}, 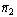 = {1, 1},
= {1, 1}, 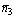 = {- 6, 4}. Так как координаты и пропорциональны 3/( — 6) = — 2/3 и — 2/4 1/( — 3), то l 1 || l 3. Для и имеем: 1/(- 6)1/4, следовательно, l 2 и l 3 пересекаются.
= {- 6, 4}. Так как координаты и пропорциональны 3/( — 6) = — 2/3 и — 2/4 1/( — 3), то l 1 || l 3. Для и имеем: 1/(- 6)1/4, следовательно, l 2 и l 3 пересекаются.