Пример 1. Плоская синусоидальная волна распространяется вдоль прямой, совпадающей с положительным направлением оси х в среде, не поглощающей энергию, со скоростью v = 15 м/с. Две точки, находящиеся на этой прямой на расстояниях х1 = 5 м и х2 = 5,5 м от источника колебаний, колеблются с разностью фаз Dj = p/5. Амплитуда волны А = 4 см. Определить: 1) длину волны; 2) уравнение волны; 3) смещение (x1) первой точки в момент времени t = 3 c.
Дано: v = 15 м/с; х1 = 5 м; х2 = 5,5 м; Dj =p/5; А = 4 см = 0,04 м; t = 3 c.
Определить: 1) l; 2) x(х,t); 3) x1.
Решение. Разность фаз колебаний двух точек волны равна:
![]() ,
,
где ![]() – расстояние между этими точками.
– расстояние между этими точками.
Тогда
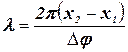 .
.
Циклическая частота ![]() , где
, где ![]() . Следовательно,
. Следовательно, ![]() .
.
Уравнение плоской синусоидальной волны, распространяющейся вдоль положительного направления оси х, имеет вид:
![]() .
.
Чтобы найти смещение (x1), надо в это уравнение подставить значения t и х.
Вычисляя, получим: 1) l = 5 м; 2) 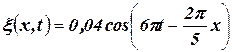 ; 3) x1 = 4 см.
; 3) x1 = 4 см.
Пример 2. Неподвижный приемник при приближении источника звука, излучающего волны с частотой n0 = 360 Гц, регистрирует звуковые колебания с частотой n = 400 Гц. Принимая температуру воздуха Т = 290 К, его молярную массу М = 0,029 кг/моль, определить скорость движения источника звука.
Дано: n0 = 360 Гц; n = 400 Гц; Т = 290 К; М = 0,029 кг/моль.
Определить: vист.
Решение. Исходя из общей формулы для эффекта Доплера в акустике и учитывая, что приемник покоится, а источник приближается к приемнику, получим:
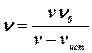 ,
,
где v – скорость распространения звука. Отсюда
![]() . (1)
. (1)
Скорость распространения звуковых волн в газах равна:
![]() , (2)
, (2)
где для воздуха ![]() .
.
Подставив (2) в (1), найдем искомую скорость движения источника звука:
![]() .
.
Вычисляя, получим: vист = 34,1 м/с.