Пусть в пространстве задана прямоугольная система координат: 0 — начало координат,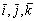 — единичные направляющие векторы осей координат, соответственно 0 х , 0 у и 0 z . Рассмотрим в пространстве произвольную плоскость
— единичные направляющие векторы осей координат, соответственно 0 х , 0 у и 0 z . Рассмотрим в пространстве произвольную плоскость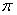 . Выведем уравнение этой плоскости, т.е. уравнение, содержащее переменные х , у , z , которому удовлетворяют координаты любой точки, лежащей на плоскости
. Выведем уравнение этой плоскости, т.е. уравнение, содержащее переменные х , у , z , которому удовлетворяют координаты любой точки, лежащей на плоскости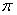 .и не удовлетворяют координаты никакой точки, не лежащей на этой плоскости.Пусть задана точка М 1( х 1, у 1, z 1)
.и не удовлетворяют координаты никакой точки, не лежащей на этой плоскости.Пусть задана точка М 1( х 1, у 1, z 1)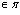 . и вектор
. и вектор 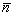 . = { А , В , C } перпендикулярный плоскости
. = { А , В , C } перпендикулярный плоскости 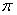 . (нормальный вектор плоскости). Пусть M ( x , у , z ) — произвольная точка, принадлежащая плоскости
. (нормальный вектор плоскости). Пусть M ( x , у , z ) — произвольная точка, принадлежащая плоскости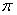 . . Тогда вектор
. . Тогда вектор
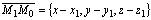
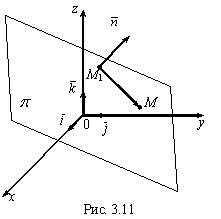
перпендикулярен вектору 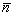 (рис. 3.11), а поэтому
(рис. 3.11), а поэтому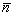
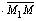 = 0 (условие перпендикулярности векторов (см. разд. 2.4)) или
= 0 (условие перпендикулярности векторов (см. разд. 2.4)) или
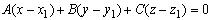
. (3.11)
Итак, координаты любой точки М , лежащей в плоскости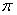 , удовлетворяют этому уравнению и , легко видеть, что координаты точки, не лежащей в плоскости
, удовлетворяют этому уравнению и , легко видеть, что координаты точки, не лежащей в плоскости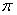 , не удовлетворяют уравнению (3.11). Следовательно, уравнение (3.11) является уравнением плоскости и называется уравнением плоскости по точке и нормальному вектору .Уравнение (3.11) является уравнением первой степени относительно текущих координат х , у , z . Можно показать (аналогично тому, как это было сделано в разд. 3.1), что всякое уравнение первой степени относительно x , у , z
, не удовлетворяют уравнению (3.11). Следовательно, уравнение (3.11) является уравнением плоскости и называется уравнением плоскости по точке и нормальному вектору .Уравнение (3.11) является уравнением первой степени относительно текущих координат х , у , z . Можно показать (аналогично тому, как это было сделано в разд. 3.1), что всякое уравнение первой степени относительно x , у , z
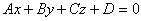
(3.12)
является уравнением некоторой плоскости (оно называется общим уравнением плоскости), причем вектор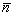 = { А , В , C }, является нормальным вектором плоскости.
= { А , В , C }, является нормальным вектором плоскости.
Если в уравнении (3.12) D = 0, то этому уравнению удовлетворяет тройка чисел (0, 0, 0), т.е. соответствующая плоскость проходит через начало координат. Нетрудно видеть, что плоскость 0 ху имеет уравнение , плоскость 0 xz — уравнение , a плоскость 0 yz задается уравнением .Известно, что плоскость однозначно определяется тремя точками, не лежащими на одной прямой. Пусть 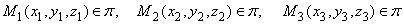 и М ( х , у , z ) — произвольная точка плоскости (рис. 3.12). Рассмотрим векторы
и М ( х , у , z ) — произвольная точка плоскости (рис. 3.12). Рассмотрим векторы
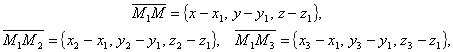
они компланарны, поэтому их смешанное произведение равно 0, т.е.
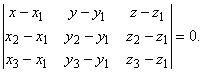
(3.13)
Это уравнение называется уравнением плоскости по трем точкам . Пусть плоскость пересекает оси координат в точках: М 1( а , 0, 0), М 2(0, b , 0), M 3(0, 0, с ). Подставляя их координаты в уравнение (3.13), находим:
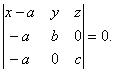
Вычислив определитель, получим:
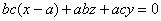
,
откуда
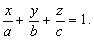
Это уравнение называется уравнением плоскости в отрезках . Пример 3.4. Построить плоскость, заданную общим уравнением:
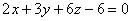
.
Решение. Преобразуем данное уравнение в уравнение в отрезках
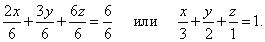

Видим, что плоскость отсекает на осях 0x , 0y , 0z , соответственно отрезки 3, 2, 1. Следовательно, она проходит через точки
М 1(3, 0, 0), М 2(0 2, 0), М 3(0, 0, 1).
По этим данным легко построить плоскость (рис. 3.13)