Пример 1. Плоская электромагнитная волна распространяется в однородной и изотропной среде с e = 2 и m = 1. Амплитуда напряженности электрического поля волны Е0 = 12 В/м. Определить: 1) фазовую скорость волны; 2) амплитуду напряженности магнитного поля волны.
Дано: e = 2; m = 1; Е0 = 12 В/м.
Определить: 1) v; 2) Н0.
Решение. Фазовая скорость электромагнитных волн равна:
,
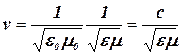где с = 3×108 м/с – скорость распространения света в вакууме.
В бегущей электромагнитной волне мгновенные значения Е и Н в любой точке связаны соотношением:
.
Тогда для амплитуд напряженностей электрического и магнитного полей волны
,
откуда искомая амплитуда напряженности магнитного поля волны равна:
.
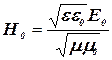Вычисляя, получим: 1) v = 2,12×108 м/с; 2) Н0 = 45 мА/м.
Пример 2. В вакууме вдоль оси x распространяется плоская электромагнитная волна. Интенсивность волны, т.е. средняя энергия, проходящая через единицу поверхности за единицу времени, составляет 21,2 мкВт/м2. Определить амплитуду напряженности электрического поля волны.
Дано: e = 1; m = 1; I = 21,2 мкВт/м2 = 2,12×10-5 Вт/м2.
Определить Е0.
Решение. Так как интенсивность электромагнитной волны определена как средняя энергия, проходящая через единицу поверхности за единицу времени, то
, (1)
где j – модуль вектора плотности потока электромагнитной энергии – модуль вектора Умова-Пойнтинга.
Согласно определению,
,
где Е и Н – соответственно мгновенные значения напряженностей электрического и магнитного полей волны, описываемые уравнениями:
;
.
Здесь Е0 и Н0 – соответственно амплитуды напряженностей электрического и магнитного полей волны; w – круговая частота; 
– волновое число (j – начальная фаза колебаний, принятая равной нулю).
Мгновенное значение модуля вектора Умова-Пойнтинга равно:
,
а его среднее значение
(2)
(учли, что 
). Записав
,
получим:
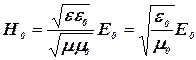(3)
(учли, что электромагнитная волна распространяется в вакууме).
Подставив (3) в (2) и учитывая (1), найдем искомую амплитуду напряженности электрического поля волны:
.
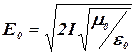Вычисляя, получим: Е0 = 126 мВ/м.