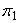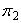Пусть плоскости и заданы общими уравнениями:

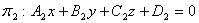
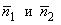- нормальные векторы этих плоскостей соответственно.Плоскост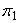и и 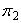параллельны или совпадают тогда и только тогда, когда векторы 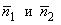коллинеарны. Записывая условие коллинеарности векторов (2.6), получаем: если 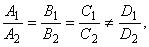то плоскости параллельны; если 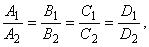то плоскости совпадают.Если же координаты векторов 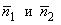не пропорциональны, то плоскости пересекаются по некоторой прямой l . Очевидно, что

.

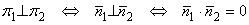
Отсюда получаем условие перпендикулярности плоскостей

.

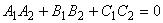
Как и для двух прямых на плоскости можно вывести следующую формулу:

,

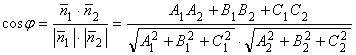
где 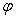— один из смежных двугранных углов между плоскостями. Расстояние d от точки М 0( х 0, у 0, z 0) до плоскости 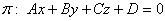вычисляется по формуле:

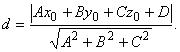
Пример 3.5. Составить уравнение плоскости 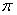, проходящей через точку M 1(- 1, 2 , 5) параллельно плоскости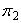: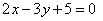. Решение. Нормальный вектор 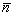={2, — 3, 0} плоскости 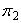является также нормальным вектором плоскости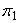. Используя равенство (3.11) получаем:

- уравнение плоскости 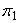по точке и нормальному вектору. Раскрывая скобки и приводя подобные слагаемые, найдем 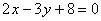— общее уравнение плоскости.