1. Объемы тел, образованных вращением криволинейной трапеции, ограниченной
кривой 
, осью 
и двумя вертикальными прямыми 
и 
, вокруг осей и 
, выражаются, соответственно, формулами
.
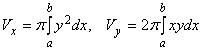Замечание. В случае иного задания уравнения кривой (параметрического, в полярных координатах и т.д.) в приведенных формулах нужно сделать соответствующие замены переменных.
2. Объем тела, полученного при вращении сектора, ограниченного дугой 
и двумя полярными радиусами 
, вокруг полярной оси, может быть вычислен по формуле
.
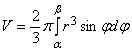Этой же формулой удобно пользоваться при отыскании объема тела, полученного вращением вокруг полярной оси фигуры, ограниченной некоторой замкнутой кривой, заданной в полярных координатах.
3. Если 
площадь сечения плоскостью, перпендикулярной к некоторой прямой (которую принимаем за ось ) в точке с абсциссой 
, то объем этого тела определяется по формуле
,
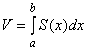где 
– абсциссы крайних сечений тела.
Пример 3.15. Вычислить объемы тел, образуемых вращением фигуры, ограниченной одной полуволной синусоиды 
и отрезком 
оси вокруг: а) оси ; б) оси .
Решение:
.
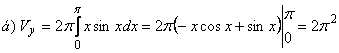Пример 3.16. Вычислить объем тела, образованного вращением кривой 
вокруг полярной оси.
Решение.
Пример 3.17. Определить объем клина, отсеченного от кругового цилиндра плоскостью, проходящей через диаметр основания и наклоненной к основанию под углом 
. Радиус цилиндра равен 
.
Решение. Примем за ось 
диаметр основания, по которому секущая плоскость пересекает основание, а за ось 
диаметр основания ему перпендикулярный. Уравнение окружности основания будет иметь вид 
(рис. 3.13). Площадь сечения АВС, отстоящего на расстоянии 
от начала координат равна
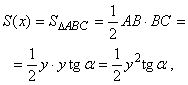
поэтому объем клина есть
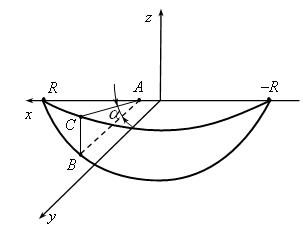
Рис. 3.13. Иллюстрация к примеру 3.17
Замечание. С помощью определенного интеграла можно решать многие физические задачи назовем некоторые из них: нахождение массы поверхности вращения, статического момента, момента инерции относительно оси или плоскости, координат центра масс; вычисление работы силы, пути, пройденного точкой при неравномерном движении по прямой с переменной скоростью и т. д.