На практике довольно часто найти точное значение определенного интеграла не удается. Например, в элементарных функциях не выражаются интегралы:
и т.д.
В этих случаях используются приближенные методы, такие как квадратурные формулы прямоугольников, трапеций, Симпсона и другие. Рассмотрим подробнее формулу Симпсона (формулу парабол)
,
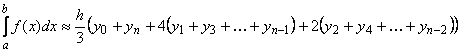где 
– четное число, 
. Погрешность этой формулы
,
где 
– наибольшее значение модуля четвертой производной интегрируемой функции 
на отрезке 
.
Пример 3.18. Вычислить приближенное значение определенного интеграла
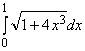
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
Решение. Разбив отрезок 
на 10 частей вычислим значения подынтегральной функции в точках разбиения
,
вычисления удобно производить в таблице (табл. 3.1).
Таблица 3.1 Вычисление интеграла из примера 3.18
|
|
|
|
|
|
|
0 |
0 |
0 |
1 |
1 |
|
1 |
0,1 |
0,001 |
1,004 |
1,002 |
|
2 |
0,2 |
0,008 |
1,032 |
1,017 |
|
3 |
0,3 |
0,027 |
1,108 |
1,053 |
|
4 |
0,4 |
0,064 |
1,256 |
1,121 |
|
5 |
0,5 |
0,125 |
1,500 |
1,225 |
|
6 |
0,6 |
0,216 |
1,864 |
1,365 |
|
7 |
0,7 |
0,343 |
2,372 |
1,540 |
|
8 |
0,8 |
0,512 |
3,048 |
1,746 |
|
9 |
0,9 |
0,729 |
3,916 |
1,979 |
|
10 |
1 |
1 |
5 |
2,236 |
Используя данные табл. 3.1, получаем
;
;
.
Подставив полученные значения в формулу Симпсона при 
, получим
.
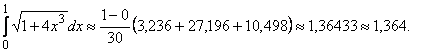