Зубчатые механизмы получили очень широкое применение в машино- и приборостроении, благодаря их большой надеж­ности и точности воспроизведения заданного закона движения.

В тех случаях, когда заданное передаточное отношение бо­льше допустимого для одной пары колес или когда требует­ся обеспечить большое межосевое расстояние, используют слож­ные механизмы, состоящие из нескольких параллельно или после­довательно соединенных друг с другом зубчатых передач. Разли­чают два вида таких механизмов: сложные зубчатые механизмы с неподвижными осями (многократные зубчатые передачи) и плане­тарные (эпициклические) механизмы, оси отдельных колес кото­рых  могут перемещаться относительно стойки. Каждый из этих видов сложных зубчатых механизмов может быть составлен не толь­ко из однородных колес (цилиндрических или конических) и пере­дач (с неподвижными осями или планетарных), но и из  их соче­тания. Наибольшее распространение получили сложные зубчатые механизмы, составленные из цилиндрических колес с прямыми зу­бьями (реже косыми) с равноделенным шагом.

Передаточное отношение одной пары цилиндрических колес

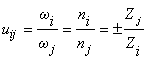   ,                                           (4.1)

где w_I , w_j -угловая скорость колес; n _i, n _j — частота вращения колес; Z_i, Z_j - числа зубьев колес i и j.

Для внешнего зацепления — отношение отрицательное (коле­са вращаются в разные стороны), для внутреннего зацепления — положительное (колеса вращаются в одном направлении).

Для конических и червячных зубчатых передач, в которых оси колес не параллельны, передаточное отношение определяется по формуле (4.1), знак же передаточного отношения не определяется.

Многократные зубчатые механизмы подразделяются на рядо­вые и ступенчатые.

Многократные рядовые зубчатые механизмы представляют собой последовательное соединение нескольких пар зубчатых колес, на каждой из неподвижных осей которых помещено по одному колесу (рис. 4.1).

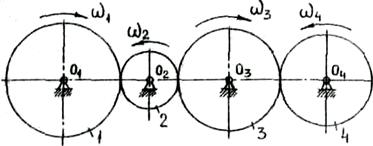
Рис. 4.1. Многократный рядовой зубчатый механизм

Общее передаточное отношение рядового зубчатого механиз­ма при n колесах равно:

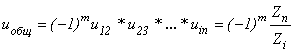,                              (4.2)

где m — число передач внешнего зацепления.

При четном m   u_общ > О, т.е. ведомое и ведущее звенья механизма вращаются в одном направлении, при нечетном m — в разных направлениях.

Из формулы (4.2) следует, что число зубьев промежуточных (паразитных) колес не влияет на значение общего передаточного отношения механизма. Установка таких промежуточных колес поз­воляет изменять направление вращения ведомого звена, устанавли­вать по нашему усмотрению расстояние между центрами крайних колес.

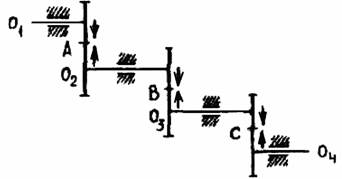
Многократные ступенчатые зубчатые механизмы представляют собой последовательное соединение нескольких пар колес, на каждой из осей которого помещено более одного колеса (кроме осей ведущего и ведомого колес) (рис. 4.2).

Общее передаточное отношение ступенчатого зубчатого меха­низма, состоящего из m ступеней, определяется по формуле

u _общ = u₁  *u₂₃ *…* u_ij ,                                               (4.3)

где m – число ступеней с внешним зацеплением зубчатых колёс.