Пример. Даны векторы: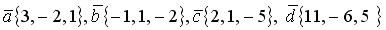 в некотором базисе. Показать, что векторы
в некотором базисе. Показать, что векторы 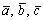 образуют базис, и найти координаты вектора
образуют базис, и найти координаты вектора 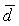 в этом базисе.
в этом базисе.
Решение. Составим определитель из координат векторов 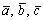 и вычислим его разложением, например, по первой строке:
и вычислим его разложением, например, по первой строке:
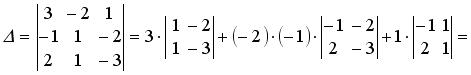
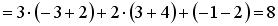
.
Так как 0, то векторы 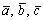 образуют базис (см. разд. 1.9).Найдем координаты вектора
образуют базис (см. разд. 1.9).Найдем координаты вектора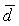 относительно базиса
относительно базиса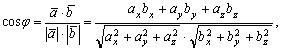 , т.е. числовые коэффициенты 1 , 2 , 3 разложения
, т.е. числовые коэффициенты 1 , 2 , 3 разложения
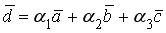
или
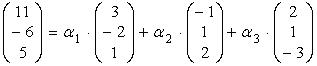
.
В силу определения равенства векторов и определения операций сложения векторов и умножения вектора на число, когда известны координаты векторов относительно некоторого базиса, последнее векторное равенство можно записать в виде системы трех линейных уравнений с тремя неизвестными:
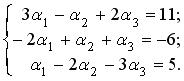
Решая эту систему, например, по формулам Крамера, находим:
1 = 2 , 2 = 3 , 3 = 1.
Ответ: .
.