В изотропной теплопроводящей среде распространение тепла описывается следующим законом Фурье: если ![]() – температура среды в точке P в момент t, то через любую площадку
– температура среды в точке P в момент t, то через любую площадку ![]() в направлении единичного вектора нормали
в направлении единичного вектора нормали ![]() к ней за промежуток времени от
к ней за промежуток времени от ![]() до
до ![]() проходит количество тепла, равное
проходит количество тепла, равное
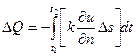 ,
,
где k – коэффициент теплопроводности, который мы будем считать постоянным; ![]() – производная функции
– производная функции ![]() по направлению вектора
по направлению вектора ![]() .
.
Тогда, количество тепла, проходящее за этот промежуток времени внутрь некоторой замкнутой поверхности ![]() , ограничивающей область
, ограничивающей область ![]() , будет равно:
, будет равно:
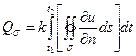 .
.
Так как ![]() , где
, где ![]() ,
, ![]() – проекция этого вектора на направление нормали, то по теореме Остроградского-Гаусса получим:
– проекция этого вектора на направление нормали, то по теореме Остроградского-Гаусса получим:
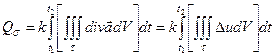 ,
,
поскольку
![]() .
.
В области ![]() могут находиться источники тепла, плотность мощностей которых обозначим
могут находиться источники тепла, плотность мощностей которых обозначим ![]() , тогда за рассматриваемый промежуток времени в области
, тогда за рассматриваемый промежуток времени в области ![]() за счет этих источников возникает количество тепла, равное:
за счет этих источников возникает количество тепла, равное:
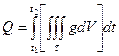 .
.
Общее количество тепла ![]() может быть подсчитано еще и другим способом, исходя из изменения температуры в точках области
может быть подсчитано еще и другим способом, исходя из изменения температуры в точках области ![]() . На изменение температуры малого объема
. На изменение температуры малого объема ![]() от
от ![]() до
до ![]() требуется количество тепла, равное:
требуется количество тепла, равное:
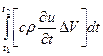 ,
,
где c – теплоемкость среды, отнесенная к единице массы, и ![]() – объемная плотность среды (будем считать c и
– объемная плотность среды (будем считать c и ![]() постоянными).
постоянными).
Это означает, что общее количество тепла, необходимое для изменения температуры во всех точках области ![]() , равно:
, равно:
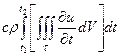 .
.
Таким образом, приравнивая выражения для общего количества тепла, полученные двумя различными способами, будем иметь:
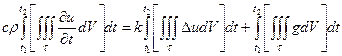
или
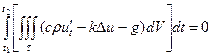 .
.
Так как промежуток времени ![]() произволен, то отсюда следует, что в любой момент времени
произволен, то отсюда следует, что в любой момент времени
![]() ,
,
а так как область ![]() произвольна, то в любой точке среды в любой момент времени должно выполняться равенство:
произвольна, то в любой точке среды в любой момент времени должно выполняться равенство:
![]()
или
![]() , (4.64)
, (4.64)
где ![]() – коэффициент температуропроводности.
– коэффициент температуропроводности.
Уравнение (4.64) является неоднородным уравнением параболического типа и называется уравнением теплопроводности. Если ![]() , то уравнение называется однородным.
, то уравнение называется однородным.
Рассмотрим тонкий теплопроводящий стержень, боковая поверхность которого теплоизолирована. Теплоизолированность боковой поверхности стержня означает, что через поверхность не происходит теплообмена с окружающей средой. Стержень предполагается настолько тонким, что в каждый момент времени температура всех точек одного и того же поперечного сечения стержня будет одной и той же. Если принять ось стержня за ось абсцисс, то температура (u)будет являться функцией координаты x и времени (t). Тогда уравнение (4.64) примет вид:
![]() . (4.65)
. (4.65)
Уравнение (4.65) называется одномерным уравнением теплопроводности.