Пример 1. Вычислить координаты вершин ромба, если известны уравнения двух его сторон: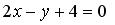 и и уравнение одной из его диагоналей: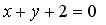 . Решение. Выясним взаимное расположение известных сторон ромба. Угловой коэффициент k прямой 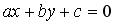определяется по формуле:

.

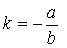
Стороны параллельны, так как имеют одинаковый угловой коэффициент:

.

Для построения рисунка (рис. 4.1) запишем уравнения в отрезках для данных прямых:

Наметим план решения: 1) находим вершины ромба P и Q ; 2) находим точку пересечения диагоналей ромба N ; 3) через точку N проводим диагональ D 2 ; 4) находим оставшиеся вершины ромба R и S .1) Так как точка P является точкой пересечения прямых L 2 и D 1 , то ее координаты находим из системы уравнений:

Из рис. 4.1 сразу находим координаты точки Q (- 2, 0) . 2) Так как диагонали ромба в точке пересечения делятся пополам, то точка является серединой отрезка PQ , поэтому ее координаты — полусумма соответствующих координат точек P и Q :

.

3) Так как диагонали ромба взаимно перпендикулярны, то прямая D 2 перпендикулярна вектору. Найдем его координаты:

= — 2 — (- 4); 0 — 2 = {2; — 2}.

По формуле (3.1) находим уравнение диагонали D 2 как уравнение прямой, проходящей через точку N (- 3, 1) перпендикулярно вектору = {2; — 2}:

2( x — (- 3)) + (- 2)( y — 1) = 0, x — y + 4 = 0.

4) Вершины ромба R и S — точки пересечения прямых L 2 и D 2 , L 1 и D 2 , соответственно, находим из уравнений:

, , , .

Ответ: P (- 4, 2) R (- 6, — 2), Q (- 2, 0), S (0, 4). Пример 2. Составить уравнения сторон треугольника, зная одну его вершину P (2, — 7), уравнения высоты 3 x + y + 11 = 0 и медианы x + 2 y + 7 = 0, проведенных из разных вершин. Решение. Для построения рисунка (рис. 4.2) приведем уравнения данных прямых к уравнениям в отрезках:

h : 3 x + y + 11 = 0, m : x + 2 y + 7 = 0 ,

План решения:1) находим уравнение прямой PQ ;2) находим координаты точки R ;3) находим уравнения прямых RP и RQ .1) Находим нормальный вектор прямой h :. Уравнение стороны PQ , проходящей через точку P (2, — 7) параллельно вектору, запишем в виде:

, x — 3 y — 23 = 0 .

Находим координаты точки Q — точки пересечения прямых PQ и m :

x = 5 , y = — 6.

2) По свойству медианы треугольника PQR точка S ( x S , y S ) является серединой отрезка RP . Следовательно:

, .

Точка S лежит на медиане m , значит,

Точка R лежит на высоте h , значит,

Из последних двух уравнений определяем координаты точки R , решая систему:

3) Используя формулу (3.4), составим уравнение прямой RP , проходящей через две заданные точки R и P :Аналогично, составим уравнение прямой RQ : Ответ: x — 3 y — 23 = 0, ,