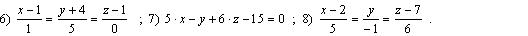Пример. Даны координаты вершин пирамиды A 1 , A 2 , A 3 , A 4:

A 1(1, — 4, 1), A 2(2, 1, 1), A 3(1, 2, 2) , A 4(2, 0, 7).

Найти:1) длину ребра A 1 A 2; 2) угол между ребрами A 1 A 2 и A 1 A 4;3) угол между ребром A 1 A 4 и гранью A 1 A 2 A 3;4) площадь грани A 1 A 2 A 3;5) объем пирамиды;6) уравнение прямой A 1 A 2;7) уравнение плоскости A 1 A 2 A 3;8) уравнение высоты, опущенной из вершины A 4 на грань A 1 A 2 A 3 . Сделать чертеж. Решение 1) Длина ребра A 1 A 2 равняется расстоянию между точками A 1 и A 2, вычисляется по формуле:

.

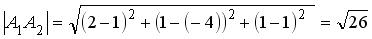2) Найдем координаты векторов и, вычитая из координат конца каждого вектора соответствующие координаты начала:

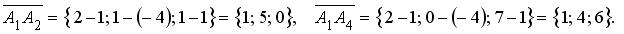
По формуле (2.10) определяем косинус угла между векторам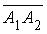и и: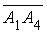

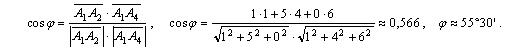
При решении заданий пунктов 3, 4, 7, 8 полезно найти какой-либо вектор, перпендикулярный плоскости A 1 A 2 A 3. В качестве такого вектора можно взять векторное произведение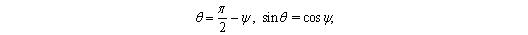.Найдем координаты векторов и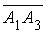

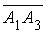= 1 — 1; 2 — (- 4); 2 — 1 = 0; 6; 1.

Координаты вектора находим по формуле (1.5):

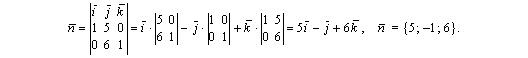
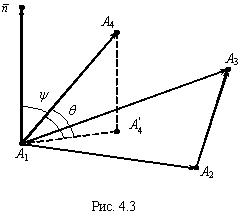На рис. 4.3 точка — проекция точки A 4 на грань A 1 A 2 A 3 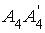, — высота, опущенная из вершины A 4 на грань A 1 A 2 A 3 .3) Угол — угол между ребром A 1 A 4 и гранью A 1 A 2 A 3 , — угол между векторам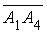и и 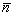. Если эти векторы лежат по одну сторону плоскости A 1 A 2 A 3 , то (см. рис. 4.3)

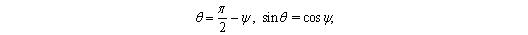
а если по разные стороны, то

Объединяем оба возможных случая единой формулой:

sin = cos .

Следовательно,

.

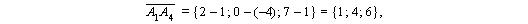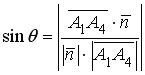
Определим угол :

;

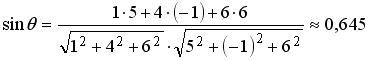40о12′ (находим по таблицам).

4) Длина векторного произведения 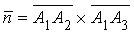равна площади параллелограмма, построенного на векторах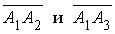, поэтому площадь треугольника A 1 A 2 A 3 (см. рис. 4.3) равна:

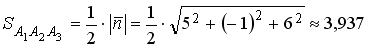(eд2).

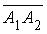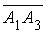
5) Объем пирамиды, построенной на векторах, 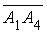равен одной шестой объема параллелепипеда, построенного на тех же векторах. Объем параллеле

пипеда, построенного на векторах, равен абсолютной величине смешанного произведения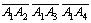. Таким образом, используя формулу (2.13), находим объем пирамиды A 1 A 2 A 3 A 4 :

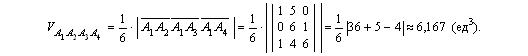
Этот объем можно найти и по другому, так как по определению смешанного произведения векторов 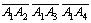=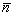, 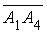то

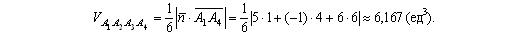
6) Используя формулу (3.5), находим уравнение прямой A 1 A 2 , проходящей через две заданные точки A 1 и A 2

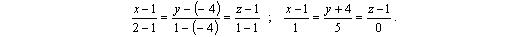
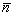:7) Используя формулу (3.11), находим уравнение плоскости A 1 A 2 A 3 , проходящей через точку A 1 (1, — 4, 1) перпендикулярно вектору 5; — 1; 6:

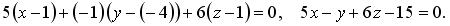
8) Используя формулу (3.15), находим уравнение высоты (см. рис. 4.3) как уравнение прямой, проходящей через точку A 4 (2, 0, 7) параллельно вектору 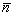5; — 1; 6:

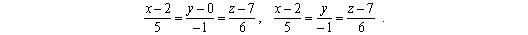
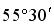Ответы: 1) 5,099; 2); 3) 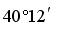; 4) 3,937; 5) 6,167;