Пример 1. Проверить удовлетворяет ли указанному уравнению данная функция z = f(x,y).
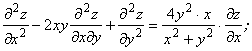
![]()
Решение. Находим частные производные первого и второго порядка:
![]()
![]()
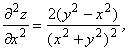
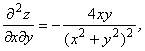
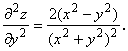
Подставляем полученные значения производных в левую часть исходного уравнения:
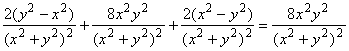 .
.
В правой части уравнения имеем:
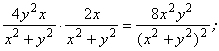
Сравнивая полученные результаты, видим, что данная функция удовлетворяет исходному уравнению.
Пример 2. Вычислить приближенно данные выражения, заменив приращения соответствующих функций их полными дифференциалами. Оценить в процентах возникающую при этом относительную погрешность вычислений.
а) ![]()
б) ![]()
Решение. а) Рассмотрим функцию ![]()
Значение этой функции в точке ![]() известно и равно
известно и равно
![]()
![]()
Вычислим приближенно значение функции по формуле:
![]()
![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]()
![]()
![]()
![]()
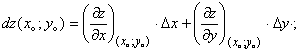
![]() ;
; ![]() .
.
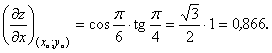
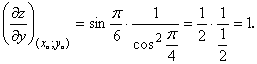
Таким образом, имеем
![]()
Относительная погрешность вычислений:
![]()
![]()
б)![]()
Рассмотрим функцию ![]()
При ![]() и
и ![]() имеем
имеем ![]()
![]() ,
, ![]()
Находим полный дифференциал функции ![]() :
:
![]()
![]()
Тогда ![]()
Относительная погрешность ![]()
Пример 3. Задана функция z = f(x,y).
1. Исследовать функцию на экстремум.
2. Найти наибольшее и наименьшее значения функции в замкнутой области D,ограниченной заданными линиями ![]() ; D:
; D: ![]() .
.
Решение.
1). Запишем необходимые условия существования экстремума
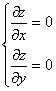
Так как в данном случае ![]() и
и ![]() всегда существуют, то для нахождения стационарных точек получаем систему уравнений
всегда существуют, то для нахождения стационарных точек получаем систему уравнений
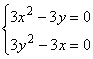 , где
, где ![]() ,
, ![]() .
.
Решаем систему уравнений
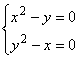 , отсюда
, отсюда ![]()
Таким образом, получим две стационарные точки ![]() и
и ![]()
 Находим:
Находим:
![]() ,
, ![]() ,
, 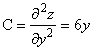
Тогда ![]()
В точке ![]()
![]() , т.е. в этой точке экстремума нет.
, т.е. в этой точке экстремума нет.
В точке ![]()
![]() и
и ![]() , следовательно, в этой точке функция достигает локального минимума
, следовательно, в этой точке функция достигает локального минимума ![]() .
.
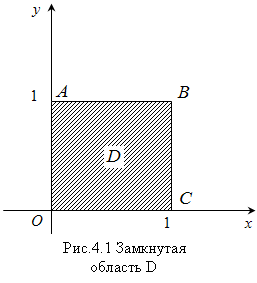
2)
а) Изображаем область D: ![]()
б) Находим критические (стационарные) точки (см. п.1) z = x2
![]() ,
, ![]()
в) Находим значение функции в этих точках.
![]()
г) Исследуем функцию на границе области, которая состоит из отрезков ОА, АВ, ВС, ОС.
На прямой ОА, где x=0, имеем z=0
На прямой АВ, где у = 1, ![]() имеем
имеем ![]() и задача сводится к отысканию наибольшего и наименьшего значений функции одной переменной на отрезке [0;1].
и задача сводится к отысканию наибольшего и наименьшего значений функции одной переменной на отрезке [0;1].
Находим
![]()
![]()
![]() ,
, ![]()
![]() ,
, ![]() ,
, ![]()
Получаем точку ![]() и z(1,1)=-1.
и z(1,1)=-1.
На прямой BC x=1,![]() получим
получим
z=1+y3 – 3y;
z′y=3y2-3;
3x2=3
y1=1, y2=-1, ![]() .Получаем точку
.Получаем точку ![]() , совпадающую с точкой локального минимума
, совпадающую с точкой локального минимума ![]() .
.
На прямой ОС, где у = 0, ![]() получим
получим ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Получим точку
. Получим точку ![]() совпадающую с одной из критических точек.
совпадающую с одной из критических точек. ![]() .
.
д) Таким образом, сравнивая все полученные значения, видим, что в замкнутой области D наибольшим значением является ![]() , а наименьшим
, а наименьшим ![]()
Пример 4. Дана функция z=f(x,y), точка А![]() , вектор
, вектор ![]() .
.
Найти:
1) ![]() т. А
т. А
2) Производную по направлению вектора ![]()
3) Записать уравнение касательной плоскости и нормали к поверхности z=f(x,y)
![]() ,
, ![]() ,
, ![]() ;
;
Решение.
1) 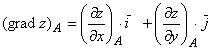
![]()
![]()
![]()
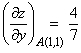
![]()
2) 
![]() ,
,![]() ;
; ![]() ;
; ![]()
Получим: ![]()
3) Уравнение касательной плоскости в т. ![]() имеет вид:
имеет вид:
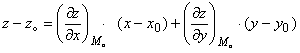 ,
,
А уравнение нормали: 
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]() ; откуда получаем
; откуда получаем ![]() – уравнение касательной плоскости.
– уравнение касательной плоскости.
![]() –уравнение нормали.
–уравнение нормали.
Пример 5. Экспериментально получены пять значений искомой функции у = f(х) при пяти значениях аргумента, которые представлены в таблице. Методом наименьших квадратов найти функцию y =f(x) в виде у = ах + b.
|
x |
1 |
2 |
3 |
4 |
5 |
|
y |
5 |
5,1 |
5,2 |
4,8 |
5,4 |
Решение. В случае линейной зависимости, т.е. если мы будем искать функцию вида ![]() , получаем нормальную систему метода наименьших квадратов:
, получаем нормальную систему метода наименьших квадратов:
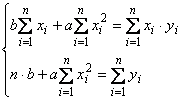
Вычисляем:
![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Система определения имеет вид:![]()
![]()
Отсюда ![]() ,
, ![]()
Следовательно ![]() .
.
Пример 6. Вычислить неопределенные интегралы:
![]()
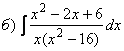
![]()
![]()
Решение. ![]() =
=
Так как ![]() , то интеграл принимает вид
, то интеграл принимает вид
![]()
сделаем замену ![]()

![]()
![]()
вернемся к первоначальной переменной ![]() :
:
![]()
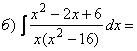
подынтегральная функция 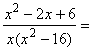
есть правильная дробь, разложим знаменатель на линейные множители, а затем дробь на простейшие
![]() ,
,
найдем ![]() методом неопределенных коэффициентов:
методом неопределенных коэффициентов:
![]() ,
,
пусть ![]() , тогда
, тогда ![]() , т.е.
, т.е. ![]()
пусть ![]() , тогда
, тогда ![]() , т.е.
, т.е. ![]()
пусть ![]() , тогда
, тогда ![]() , т.е.
, т.е. ![]()
и интеграл принимает вид:
![]() .
.
![]()
сделаем универсальную тригонометрическую подстановку
![]() , так как
, так как ![]() , тогда подынтегральная функция принимает вид
, тогда подынтегральная функция принимает вид
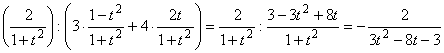 ,
,
а интеграл принимает вид

![]() .
.
![]()
сделаем замену переменной ![]() , тогда
, тогда ![]() , а чтобы найти
, а чтобы найти ![]() найдем дифференциал от обеих частей равенства
найдем дифференциал от обеих частей равенства ![]() ,
,
т.е. ![]() и интеграл принимает вид
и интеграл принимает вид
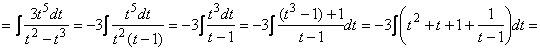
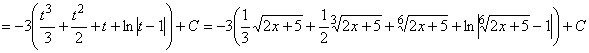 .
.
Пример 7. Вычислить приближенное значение определенного интеграла
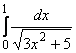
с помощью формулы Симпсона, разбив отрезок интегрирования на 10 частей. Все вычисления производить с округлением до третьего десятичного знака.
Решение. Разбив отрезок ![]() на 10 частей, вычислим значения подынтегральной функции в точках разбиения
на 10 частей, вычислим значения подынтегральной функции в точках разбиения
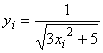 ,
,
вычисления удобно производить в таблице (табл. 4.1).
Таблица 4.1 Значения подынтегральной функции в точках разбиения
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
5 |
2,236 |
0,447 |
|
1 |
0,1 |
0,01 |
0,03 |
5,03 |
2,243 |
0,446 |
|
2 |
0,2 |
0,04 |
0,12 |
5,12 |
2,263 |
0,442 |
|
3 |
0,3 |
0,09 |
0,27 |
5,27 |
2,296 |
0,436 |
|
4 |
0,4 |
0,16 |
0,48 |
5,48 |
2,341 |
0,427 |
|
5 |
0,5 |
0,25 |
0,75 |
5,75 |
2,398 |
0,417 |
|
6 |
0,6 |
0,36 |
1,08 |
6,08 |
2,466 |
0,406 |
|
7 |
0,7 |
0,49 |
1,47 |
6,47 |
2,544 |
0,393 |
|
8 |
0,8 |
0,64 |
1,92 |
6,92 |
2,631 |
0,380 |
|
9 |
0,9 |
0,81 |
2,43 |
7,43 |
2,726 |
0,367 |
|
10 |
1 |
1 |
3 |
8 |
2,828 |
0,354 |
Используя данные табл. 4.1, получаем
![]() ;
;
![]() ;
;
![]() .
.
Подставив полученные значения в формулу Симпсона при ![]() , получим
, получим
 .
.
Пример 8. Вычислить несобственный интеграл ![]() или доказать его расходимость.
или доказать его расходимость.
Решение. Подынтегральная функция разрывна в точке![]() . По определению
. По определению
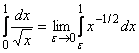 .
.
По формуле Ньютона-Лейбница
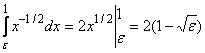 ,тогда
,тогда  .
.
Пример 9. Найти длину дуги кривой ![]()
Решение. 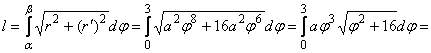
![]()
![]()
Пример 10. Найти площадь поверхности, образованной вращением петли кривой ![]() вокруг оси
вокруг оси![]() .
.

Рис. 4.2 Вращение петли кривой ![]()
Решение. Петля кривой соответствует значениям ![]() Введем параметр
Введем параметр ![]() , полагая
, полагая ![]() , и зададим кривую параметрически уравнениями
, и зададим кривую параметрически уравнениями ![]() . Дуга NPOMN (петля) кривой соответствует значениям
. Дуга NPOMN (петля) кривой соответствует значениям
![]() .
.

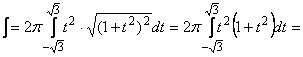
![]()
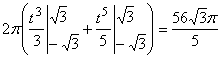 .
.