Процесс нагревания или охлаждения может происходить при различных условиях. Рассмотрим процесс нагревания газа одного и того же количества (1 кг) в одинаковых цилиндрах с одинаковыми начальными параметрами (рис. 5.1).

В обоих цилиндрах газ будем нагревать до одинаковой температуры Т₂. В первом цилиндре (рис.5.1, а) теплота будет подводиться при постоянном объеме, т.е. процесс будет изохорным. Во втором цилиндре (рис.5.1, б) газ будет расширяться от v₁ до v₂ при постоянном давлении (р), т.е. процесс будет изобарным.

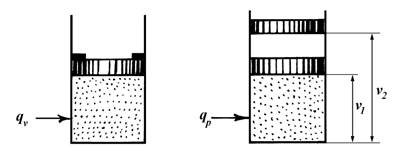
Рис. 5.1. Изохорный (а) и изобарный (б) процессы

Так как в первом случае газ не расширяется, он не совершает работу и поэтому вся подводимая теплота тратится на повышение внутренней энергии и на повышения давления. Удельное количество теплоты можно определить по формуле:

.

Во втором цилиндре подведенная к газу теплота расходуется как на повышение температуры, так и на перемещение поршня (т.е. на совершение работы). Удельное количество теплоты в этом случае можно определить по формуле:

.                            (5.2)

Подогрев газа в обоих цилиндрах идет до одинаковой температуры Т₂, но во втором случае теплоты необходимо затратить больше на величину работы l, совершенной для перемещения поршня. Тогда:

                  или                 .

Известно, что работа (l) при р = const составляет:

              или                 .

Так как , то . Следовательно, имеем:

.

откуда

.                            (5.3)

Полученная связь между изобарной и изохорной теплоемкостями (5.3) называется уравнением Майера. Зная зависимость между теплоемкостями, можно записать:

.

Таким образом, в зависимости от того к какой количественной единице вещества относится теплоемкость, различают следующие виды изобарной и изохорной теплоемкостей:

 – массовые изобарная и изохорная теплоемкости;

 – объемные изобарная и изохорная теплоемкости;

 – мольные изобарная и изохорная теплоемкости.

В термодинамических расчетах часто встречается величина (), называемая показателем адиабаты и равная отношению изобарной теплоемкости к изохорной:

.

Значение показателя адиабаты зависит от температуры, но для газов и паров эта зависимость незначительна, и ею пренебрегают, принимая  величиной постоянной. Для идеальных газов значение показателя адиабаты принимают равным:

· одноатомных газов – 1,67;

· двухатомных газов – 1,4;

· трех- и многоатомных газов – 1,29.

Точные значения  для некоторых газов и водяных паров приводятся в справочниках в зависимости от их температур.