Проводится тестирование программной системы двумя совершенно независимыми группами, использующими независимые наборы тестов. Эти две группы тестируют систему параллельно в течение некоторого времени; затем их результаты собирают и сравнивают.
Пусть N1 и N2 – число ошибок, обнаруженных каждой из групп, соответственно, N12 – число ошибок, обнаруженных дважды (т.е. обеими группами), N – неизвестное полное число ошибок в программе.
Это можно проиллюстрировать следующим образом (рис. 5.3).
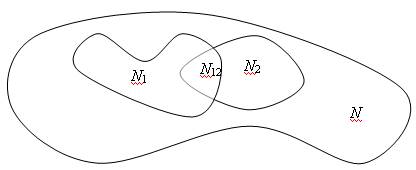
Рис. 5.3. Множества ошибок, обнаруженных на независимых тестах
Тогда эффективность тестирования каждой из групп: ![]() .
.
Исходя из предположения, что возможность обнаружения для всех ошибок одинакова, каждое подмножество пространства N рассматривается как аппроксимация всего пространства.
Т.е. ![]() , подставляем
, подставляем ![]() , получаем
, получаем ![]() . Выражая из последней формулы N, получаем
. Выражая из последней формулы N, получаем
![]() .
.
В полученной формуле N12 известно, Е1 и Е2 можно оценить как N12/ N2 и N12/ N1, соответственно, и получить приближение для N.
Например, пусть две группы нашли по 20 и 30 ошибок, соответственно, пусть 8 ошибок – общие, тогда Е1 = 0.27, Е2 = 0.4, N = 74 и примерно осталось 32 необнаруженных ошибки (74 – 30 – 20 + 8).