Мы рассматривали до сих пор задние углы фасонной фрезы в плоскости, перпендикулярной оси фрезы. Однако при ее проектировании необходимо иметь формулы для задних углов в других сечениях, например, в нормальном. Получим связь между углами в нормальном и продольном сечениях. На рис. 6.30: 00 – сечение, перпендикулярное оси фрезы; ММ – касательная плоскость в точке С; NN – нормальное сечение;   — угол в плоскости 00,  — задний угол в плоскости NN;  — угол между касательной к профилю фрезы и линией (плоскостью), перпендикулярной к оси фрезы.

.                                                                                                    (6.13)

Для любой точки профиля фрезы при затыловании по спирали Архимеда

.

Если R-h=r – радиус любой точки (С) на профиле, то

.                                                                                                (6.14)

Из формулы (6.14) видно, что  с уменьшением угла  уменьшается и при  угол =0. Для нормальной работы фрезы необходимо принять =2…3⁰, а затем аналитически или графически определить угол  для самой неблагоприятной точки боковой кромки.

Если  оказывается меньшим 5⁰, то его необходимо увеличить искусственным путем, например, выполнить скосы под углом 10⁰ (рис.6.31).

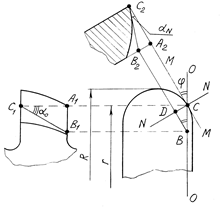
Рис. 6.30. Задний угол в нормальном сечении затылованной фрезы

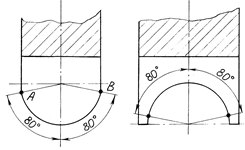
Рис. 6.31. Формы зубьев полукруглых фрез