При изучении качественных показателей часто приходится рассматривать изменение во времени (пространстве) средней величины индексируемого показателя для определенной однородной совокупности.

Средняя величина является сводной характеристикой качественного показателя и складывается под влиянием значений показателя у индивидуальных элементов (единиц), из которых состоит совокупность и под влиянием их весов (структуры совокупности).

Если любой качественный индексируемый показатель обозначить через х, а его веса через f, то динамику среднего показателя можно отразить как за счет изменения обоих факторов (х и f), так и за счет каждого фактора отдельно. В результате получим три различных индекса: индекс переменного состава, индекс фиксированного (постоянного) состава и индекс структурных сдвигов.

Индекс переменного состава – отражает динамику среднего показателя за счет изменения индексируемой величины х у отдельных элементов (частей целого) и за счет изменения весов f, по которым взвешиваются отдельные значения х.

Любой индекс переменного состава – это отношение двух средних величин для однородной совокупности (за два периода или по двум территориям):

.

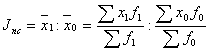Индекс фиксированного (постоянного) состава – отражает динамику среднего показателя лишь за счет изменения индексируемой величины х, при фиксировании весов на уровне, как правило, отчетного периода f₁:

.

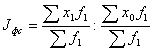Например, изменение цены на отдельных рынках (предприятиях) можно выявить с помощью индекса фиксированного (постоянного) состава:

.

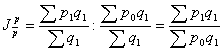Индекс постоянного состава показывает изменение средней цены за счет изменения индивидуальных цен.

Индекс структурных сдвигов – показывает динамику среднего показателя лишь за счет изменения весов f  при фиксировании индексируемой величины на уровне базисного периода х₀.

.

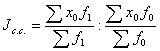Например, влияние на изменение средних цен за счет структуры покажет индекс структурных сдвигов:

.

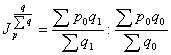Индекс структурных сдвигов показывает изменение средней цены за счет изменения структуры продаж, производства.

Между вышеперечисленными индексами существует взаимосвязь: индекс переменного состава есть произведение индекса постоянного состава на индекс структурных сдвигов:

.

Рассмотрим расчет индексов на конкретном примере.

Пример 1.

Определить: индексы себестоимости переменного и постоянного составов, индекс   структурных сдвигов. Показать взаимосвязь индексов.

1) Обозначим выработку базисного периода через q₀, отчетного периода – q₁; себестоимость изделия в базисном периоде z₀, в отчетном периоде z₁.

2)  Индекс переменного состава:

.

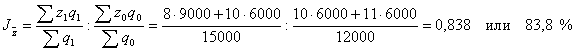Таким образом, средняя себестоимость изделия отчетного периода по сравнению с базисным уменьшилась на 16,2 % (83,8 – 100).

3)  Индекс постоянного состава:

,

.

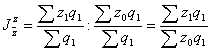Таким образом, изменение себестоимости на каждом предприятии снизило среднюю себестоимость на 15,4 % (84,6 – 100).

4)  Индекс структурных сдвигов:

.

Таким образом, средняя себестоимость уменьшилась на 0,9 % (99,1 – 100) за счет изменения структуры производства.

5)  Взаимосвязь индексов:

,

0,838 = 0,846 х 0,991.