Задачи, которые встречаются при определении количественных характеристик надежности, могут быть разбиты на следующие группы:

1) определение количественных характеристик надежности по статистическим данным об отказах изделия;

2) определение количественных характеристик надежности изделия при известном аналитическом выражении одной какой-либо характеристики.

При решении задач первой группы используются статистические определения количественных характеристик надежности, при решении задач второй группы – вероятностные определения характеристик и аналитические зависимости между ними.

Рассмотрим типовые примеры.

Пример 1

Допустим, что на испытание поставлено 1 000 однотипных электронных ламп типа 6Ж4. За 3 000 часа отказало 80 ламп. Требуется определить вероятность безотказной работы и вероятность отказа электронных ламп в течение 3 000 часов.

Решение

Определяем вероятность безотказной работы и вероятность отказа:

3 000)=0,92;

3 000)=0,08

или

3000) = 1 – P(3 000) = 1 -0,92 = 0,08.

Пример 2

На испытание было поставлено 1 000 однотипных ламп. За первые 3 000 часов отказало 80 ламп, а за интервал времени 3 000 – 4000 ч отказало еще 50 ламп. Требуется определить частоту и интенсивность отказов электронных ламп в промежутке времени 3 000 – 4 000 ч.

Решение

Найдем частоту отказов по формуле:

(3 500) =5 ч^-1

Интенсивность отказов определяем по формуле:

(3500)= 5,6 ч^-1

Пример 3

На испытание поставлено N = 400 изделий. За время t = 3 000 ч  отказало n(t) = 200 изделий, за интервал времени t = 100 ч отказало n(t)  =100 изделий. Требуется определить: 3 000),  (3 100),  (3 050), (3 050), (3 050).

Решение

Найдем вероятность безотказной работы по формуле:

(t) = .

Тогда

для t = 3000 ч:

(3 000) = = 0,5;

для t = 3100 ч:

3100) =  = 0,25.

Определим среднее число исправно работающих образцов в интервале времени t по формуле:

N_ср = =  = 150.

где N_i – число изделий, исправно работающих в начале интервала t, N_i+1 – число изделий, исправно работающих в данный отрезок времени.

Число отказавших изделий за время t = 3 050 ч равно:

n(3 500) = N – N = 400 – 150 = 250,

тогда

.

Определим частоту отказов по формуле:

 ч^-1.

Определим интенсивность отказов по формуле:

.

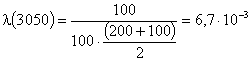Пример 4

На испытании находилось N_o = 1000 образцов неремонтируемой аппаратуры. Число отказов n(Dt) фиксировалось через каждые 100 ч работы (Dt = 100 ч). Данные об отказах приведены в таблице 8.1. Требуется вычислить количественные характеристики надежности и построить зависимости характеристик от времени.

Решение

Аппаратура относится к классу невосстанавливаемых изделий. Поэтому критериями надежности будут: P(t), T_ср, a(t), l(t).

Вычислим P(t) по формуле:

.

И построим график зависимости:

;

;

………………………………..

;

Таблица 8.1

Данные об отказах аппаратуры к примеру 4

Dti, ч	N(Dti)	Dti, ч	N(Dti)
0 – 100	50	1500 – 1600	13
100 – 200	40	1600 – 1700	13
200 – 300	32	1700 – 1800	13
300 – 400	25	1800 – 1900	14
400 -500	20	1900 – 2000	12
500 -600	17	2000 – 2100	12
600 – 700	16	2100 – 2200	13
700 – 800	16	2200 – 2300	12
800 -900	15	2300 – 2400	13
900 – 1000	14	2400 – 2500	14
1000 – 1100	15	2500 – 2600	16
1100 -1200	14	2600 – 2700	20
1200 – 1300	14	2700 – 2800	25
1300 – 1400	13	2800 – 2900	30
1400 – 1500	14	2900 – 3000	40

Рассчитаем характеристику a(t) по формуле:

.

Построим график зависимости:

;

;

…………………………………………

.

Рассчитаем l(t) по формуле:

;

;

;

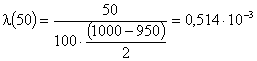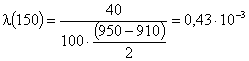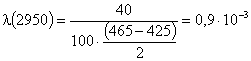
и так далее

Значения P(t), a(t), l(t), вычисленные для всех Dt_i, сведем в таблицу 8.2.

Таблица 8.2

Результаты вычислений к примеру 4

Dti, ч	P(t)	a(t), х10-3 ч	l(t), х10-3 ч
0 – 100	0,950	0,50	0,514
100 – 200	0,910	0,40	0,430
200 – 300	0,878	0,32	0,358
300 – 400	0,853	0,25	0,289
400 – 500	0,833	0,20	0,238
500 – 600	0,816	0,17	0,203
600 – 700	0,800	0,16	0,198
700 – 800	0,784	0,16	0,202
800 – 900	0,769	0,15	0,193
900 – 1000	0,755	0,14	0,184
1000 – 1100	0,740	0,15	0,200
1100 – 1200	0,726	0,14	0,191
1200 – 1300	0,712	0,14	0,195
1300 – 1400	0,699	0,13	0,184
1400 – 1500	0,685	0,14	0,262
1500 – 1600	0,672	0,13	0,192
1600 – 1700	0,659	0,13	0,195
1700 – 1800	0,646	0,13	0,200
1800 – 1900	0,632	0,14	0,220
1900 – 2000	0,620	0,12	0,192
2000 – 2100	0,608	0,12	0,195
2100 – 2200	0,595	0,13	0,217
2200 – 2300	0,583	0,12	0,204
2300 – 2400	0,570	0,14	0,225
2400 – 2500	0,556	0,16	0,248
2500 – 2600	0,540	0,16	0,290
2600 – 2700	0,520	0,20	0,376
2700 – 2800	0,495	0,25	0,490
2800 – 2900	0,465	0,30	0,624
2900 – 3000	0,425	0,40	0,900

Вычислим среднее время безотказной работы, предположив, что на испытании находились только те образцы, которые отказали. Учитывая, что в данном случае

m = t_k/Dt = 3000/100 = 30;

N₀ = 575,

имеем:

.

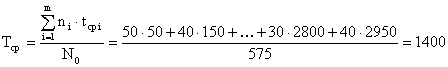Полученное значение средней наработки до первого отказа является заниженным, так как опыт был прекращен после отказа 575 образцов из 1 000, поставленных на испытание.

Пример 5

В течение некоторого периода времени производилось наблюдение за работой одного экземпляра радиолокационной станции. За весь период наблюдения было зарегистрировано 15 отказов. До начала наблюдения станция проработала 258 ч, к концу наблюдения наработка станции составила 1 233 ч. Требуется определить среднюю наработку на отказ.

Решение

Наработка радиолокационной станции за наблюдаемый период равна:

t = t_{2 –} t₁ =1 233 – 258 = 975 ч.

Принимая

,

находим среднюю наработку на отказ:

,

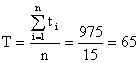где t_i – время исправной работы изделия между (i – 1)-м и i-м отказами; n – число отказов за некоторое время t.

Пример 6

За наблюдаемый период эксплуатации в аппаратуре было зафиксировано 8 отказов. Время восстановления составило:

t₁ = 12 мин;       t₂ = 23 мин;    t₃ = 15 мин;    t₄ = 9 мин;

t₅ = 15 мин;       t₆ = 28 мин;    t₇ = 25 мин;      t₈ = 31 мин.

Требуется определить среднее время восстановления аппаратуры.

Решение

Среднее время восстановления аппаратуры равно:

.

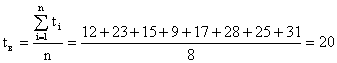Пример 7

Аппаратура имела среднюю наработку на отказ t_cр = 65 ч и среднее время восстановления t_в = 1,25 ч. Требуется определить коэффициент готовности.

Решение

Коэффициент готовности равен:

.
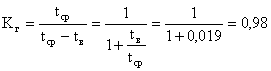