Двигатель Стирлинга – газовый двигатель поршневого типа с внешним подводом теплоты, которая получается в результате сгорания твердых, жидких, газообразных топлив. Внешний подвод теплоты осуществляется через теплопроводящую стенку. Рабочее тело (водород, гелий, аргон, углекислый газ) находится в замкнутом пространстве и во время работы не заменяется.

Одна из возможных конструктивных схем двигателя Стирлинга, когда рабочий 5 (рис. 9.29) и вытеснительный 1 поршни находятся в одном цилиндре.

В процессе перекачки в горячую полость (над рабочим поршнем) рабочее тело в регенераторе 3 и нагревателе 4 получает теплоту, а в процессе перекачки в холодную полость (под рабочим поршнем) отдает теплоту в регенераторе 3 и охладителе 2. Для осуществления этих процессов движение вытеснительного поршня 1 сдвинуто по фазе по отношению к движению рабочего поршня 5.

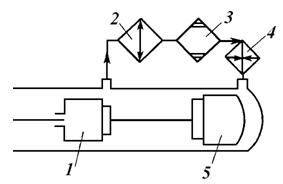
Рис. 9.29. Конструктивная схема двигателя Стирлинга

Идеальный цикл Стирлинга состоит из четырех процессов (рис. 9.30). В процессе а–с холодное рабочее тело сжимается в изотермическом процессе Т_а = Т_с = Т₂ при интенсивном отводе теплоты q₂". В процессе c–z поршень-вытеснитель перемещает рабочее тело из холодной полости в горячую, так что v_c = v_z (изохорный процесс), а температура увеличивается от Т_С = Т₂ до T_z  = T₁ при подводе теплоты q₁‘.

В изотермическом процессе расширения T_z = T_e = T₁ к рабочему телу подводится теплота q₁". Затем поршень-вытеснитель, перемещаясь в обратном направлении, выталкивает рабочее тело из горячей полости в холодную (v_e = v_a = const) с отводом теплоты q₂‘. Отличительной особенностью цикла Стирлинга является то, что рабочее

тело, перемещаясь из холодной полости в горячую и обратно через регенератор, то воспринимает теплоту от рабочего тела, то, охлаждаясь, отдает теплоту рабочему телу.

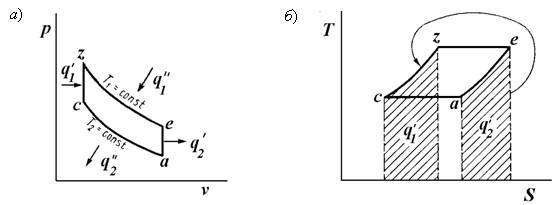
Рис. 9.30. Диаграмма работы идеального цикла Стирлинга

Работа в цикле Стирлинга представляет собой разность работы, полученной в процессе изотермического расширения (подвод теплоты q₁"), и работы, затраченной в процессе изотермического сжатия с отводом теплоты (q₂"):

.

При полной регенерации , так как

;

.

Термический КПД цикла при идеальном регенераторе равен:

.                             (9.14)

Подставив выражения для q₁" и q₂" в уравнение (9.14), получим:

.

Так как изохоры идеального газа на TS-диаграмме эквидистантны, то

.

Следовательно:

.

Таким образом, термический КПД цикла Стирлинга с полной регенерацией теплоты равен термическому КПД цикла Карно.

Если ввести параметры цикла:  = v_a/v_c – степень сжатия и – степень повышения температуры, то термический КПД цикла может быть преобразован к виду:

.

Среднее давление цикла равно:

или

.

Двигатели Стирлинга завоевали право на широкое применение. Они достигли уровня современных дизелей, а по некоторым показателям превзошли их:

· менее токсичны;

· меньше уровень шума;

· могут работать с практически любыми источниками теплоты.

Так, был создан и испытан в космическом пространстве для привода регенератора двигатель Стирлинга, в котором в качестве источника теплоты использовалась энергия солнечных лучей.