Классическими методами математической статистики можно описать влияние случайных погрешностей на результат анализа генеральной совокупности (). Генеральная совокупность характеризуется значениями среднего арифметического (m) и стандартного отклонения (s):

,              .

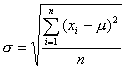Теоретически ожидаемое распределение экспериментальных результатов генеральной совокупности описывается законом нормального распределения (функцией Гаусса):

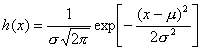         или     ,

где х – единичное измерение; h – частота появления значения х;   – отклонение единичного результата х от среднего m в единицах стандартного отклонения s.

Площадь под кривой нормального распределения ошибок, рассчитанная в пределах  показывает, что вероятность попадания единичного измерения в бесконечный интервал равна единице. Площадь под кривой Гаусса, рассчитанная в пределах , представляет вероятность того, что отклонение единичного измерения от среднего не превышает величины .

Доверительная вероятность (P_дов.) – это вероятность того, что найденное значение измеряемой величины (х) лежит в интервале . В пределах ±s будет находиться ~68,3 % значений генеральной совокупности, в пределах ±2s  –  95,5 % значений и в пределах ±3s  –  99,7 % значений.

Для выборочной совокупности с небольшим числом определений (n > 20) m и s неизвестно, вместо этих величин пользуются их оценками . Тогда для среднего из n параллельных определений:

.