Многоступенчатый компрессор применяется для получения сжатого газа высокого давления. Сжатие газа в нем осуществляется в нескольких ступенях с промежуточным охлаждением сжимаемого газа между ступенями. Охлаждение газа после каждой ступени производится при постоянном давлении.

Многоступенчатое сжатие газа позволяет:

· снизить температуру газа в конце сжатия, применяя промежуточное охлаждение, и обеспечить надежную эксплуатацию компрессора;

· понизить мощность, идущую на привод компрессора, за счет работы, сэкономленной при охлаждении газа в холодильнике.

На рис. 9.8, а дана схема двухступенчатого компрессора, а на рис. 9.8, б представлена рV-диаграмма процесса сжатия газа в обеих ступенях такого компрессора.

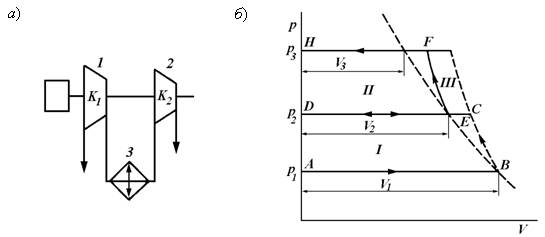
Рис. 9.8. Схема двухступенчатого компрессора (а) и рV-диаграмма процесса сжатия газа в обеих ступенях компрессора (б)

Рассмотрим рV-диаграмму двухступенчатого компрессора (рис. 9.8). Здесь А–В – всасывание газа в первую ступень; В–С – политропное сжатие в первой ступени; C–D – процесс выталкивания газа из первой ступени; D–C – процесс  поступления газа в холодильник; C-Е – процесс охлаждения в холодильнике; E–D – процесс выталкивания газа из холодильника; D–E – процесс всасывания газа во вторую ступень; E–F – политропное сжатие газа во второй ступени; F–H – процесс нагнетания газа из второй ступени к потребителю; пл. I – работа сжатия газа в первой ступени; пл. II – работа сжатия газа во второй ступени; пл. III – работа, сэкономленная при охлаждении газа в холодильнике.

При расчете многоступенчатого компрессора важно решить вопрос о распределении общего перепада давлений между ступенями. В качестве критерия целесообразно выбрать минимальную работу, затрачиваемую на привод компрессора. Если предположить, что при политропном процессе сжатия газа в каждой ступени показатель политропы будет одинаковым и температура газа в начале каждого сжатия равна первоначальной (Т₁ = Т₂), то работа двухступенчатого компрессора определяется по формуле:

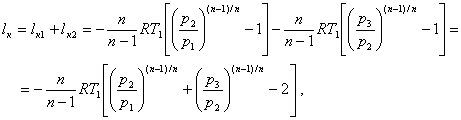
где  и  – работа сжатия в первой и во второй ступенях соответственно.

Для т ступеней сжатия

где - степень повышения давления в i-й ступени.

Оптимальное значение  для ступени компрессора найдем по методу Лагранжа из системы уравнений:

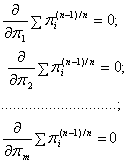
при условии

.

Из решения системы этих уравнений находим:

Минимальная работа m-ступенчатого компрессора, соответствующая оптимальным степеням повышения давления, равна:

.

На рис. 9.9, изображены ТS-диаграммы процессов адиабатного (рис. 9.9, а) и политропного сжатия газа (9.9, б) в двухступенчатом компрессоре. Линии В–С и E–F изображают процессы сжатия, линия С–Е соответствует изобарному отводу теплоты в холодильник.

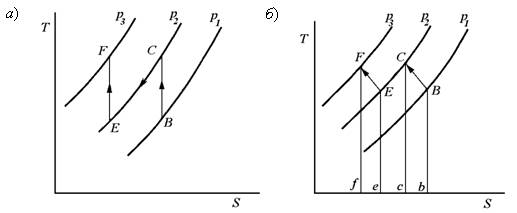
Рис. 9.9. ТS-диаграммы процессов адиабатного (а) и политропного сжатия газа (б) в двухступенчатом компрессоре

Площади ВСсbВ и EFfeE (рис. 9.9, б) изображают теплоту, отведенную от газа при политропном сжатии в отдельных цилиндрах компрессора. Так как политропы эквидистантны

(ds/dT)_p = idem (при Т = const),

то площади ВСсbВ и EFfeE равны между собой. Следовательно, количество теплоты, отводимое от газа в каждом цилиндре, будет одинаковым для обеих ступеней.