Искривленная поверхность оказывает на жидкость избыточное давление. Это давление обусловлено силами поверхностного натяжения, результирующая которых направлена внутрь жидкости. Для  выпуклой поверхности оно положительно:

.                            (9.4)

Здесь σ – поверхностное натяжение, R – радиус кривизны поверхности.

Если поверхность жидкости вогнутая, то результирующая сила поверхностного натяжения, направлена из жидкости и давление равно:

.                           (9.5)

Давление под изогнутой кривой меньше на величину Δp. Формулы (9.4) и (9.5) являются частными случаями формулы Лапласа:

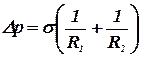,                         (9.6)

где R₁ и R₂ – радиусы кривизны двух любых взаимно перпендикулярных нормальных сечений поверхности жидкости в данной точке. Если центр кривизны сечения находится внутри жидкости, то R > 0, если центр кривизны находится вне жидкости, то R < 0.

Для сферической поверхности  R₁ = R₂  = R, и выражение (9.6) переходит в выражение (9.5). Для цилиндрической поверхности R₁ = R,   R₂ =  ∞,  соответственно . Для плоской поверхности R₁ =  R₂ =  ∞, поэтому Δp = 0.