Рекурсия – метод определения класса объектов или методов предварительным заданием одного или нескольких (обычно простых) его базовых случаев или методов, а затем заданием на их основе правила построения определяемого класса. Другими словами, рекурсия – частичное определение объекта через себя, определение объекта с использованием ранее определённых объектов. Рекурсия используется, когда можно выделить самоподобие объекта. Приведем несколько примеров рекурсии.
Рекурсия в физике. Классическим примером бесконечной рекурсии являются два поставленные друг напротив друга зеркала: в них образуются два коридора из затухающих отражений зеркал.
Рекурсия в языке и литературе. Всем известная притча «У попа была собака…» является типичной рекурсией. Несколько рассказов Станислава Лема посвящены казусам при бесконечной рекурсии. Например, рассказ о разумной машине, которая обладала достаточным умом и ленью, чтобы для решения поставленной задачи построить себе подобную, и поручить решение ей (итогом стала бесконечная рекурсия, когда каждая новая машина строила себе подобную и передавала задание ей).
Рекурсия в изобразительном искусстве. Эффект Droste – термин для изображения специфического вида рекурсивного изображения. Изображение включает уменьшенный собственный вариант самого себя (рис. 9.1). Этот более малый вариант после этого показывает даже более малый вариант себя, и так далее. Практически это продолжается пока разрешение изображение позволяет уменьшать размер. Термин был введен в честь голландского какао Droste.

Рис. 9.1. Рекурсия в изобразительном искусстве
Рекурсия в сюжете. Первым романом, удивившим читателей приемом рекурсии, был «Дон Кихот». Сервантес все время пытался смешивать два мира: мир читателя и мир книги. У Сервантеса главный процесс не просто книга, но книга плюс читатель. В шестой главе цирюльник, осматривая библиотеку Дон Кихота, находит книгу Сервантеса и высказывает суждения о писателе. Вымысел Сервантеса рассуждает о нем. В начале девятой главы сообщается, что роман переведен с арабского и что Сервантес купил его на рынке. Наконец, во второй части романа персонажи уже прочли первую часть.
Рекурсия в математике: Факториал целого неотрицательного числа n обозначается n! и определяется как
n! = n × (n – 1)! при n > 0 и n! = 1 при n = 0.
Рекурсия в программировании. Функция называется рекурсивной, если во время ее обработки возникает ее повторный вызов, либо непосредственно, либо косвенно, путем цепочки вызовов других функций. Прямой (непосредственной) рекурсией является вызов функции внутри тела этой функции. Например:
int a()
{…..a()…..}
Косвенной рекурсией является рекурсия, осуществляющая рекурсивный вызов функции посредством цепочки вызова других функций. Все функции, входящие в цепочку, тоже считаются рекурсивными. Например:
a(){…..b()…..}
b(){…..c()…..}
c(){…..a()…..}
Все функции a,b,c являются рекурсивными, так как при вызове одной из них, осуществляется вызов других и самой себя.
Приведем пример прямой рекурсии:
#include<stdio.h>
void up_and_doun(int); // Прототип функции
int main(void)
{
up_and_doun(1); // Вызов функции
return 0;
}
void up_and_doun(int n)
{
printf(“Уровень %dn”,n); // Оператор печати 1
if(n<4) up_and_doun(n+1); // Рекурсивный вызов функции
printf(“Уровень %dn”,n); // Оператор печати 2
}
Прокомментируем эту программу:
· во-первых, каждый уровень вызова функции имеет собственные переменные. Это означает, что переменная n уровня 1 отличается от переменной n уровня 2. Таким образом, программа создает четыре отдельные переменные, каждая из которых названа n, но имеет свое значение;
· во-вторых, каждому вызову соответствует возврат функции. Когда поток программы достигает оператора return в конце последнего уровня рекурсии, управление передается предшествующему уровню рекурсии. Программа должна пройти по всем уровням рекурсии, возвращаясь из одного уровня функции up_and_doun() к тому уровню этой же функции, который ее вызывал (рис. 9.2);

Рис. 9.2. Рекурсивные вызовы функции up_and_doun()
· в-третьих, операторы в рекурсивной функции, которые расположены перед рекурсивным вызовом, выполняются в том же порядке, в каком вызываются функции;
· в-четвертых, операторы рекурсивной функции, которые расположены после рекурсивного вызова, выполняются в обратном порядке по отношению к порядку вызова функций. Эта особенность рекурсии полезна при программировании задач, в которых требуется обратный порядок выполнения.
Широкое проникновение рекурсивных методов в практику программирования началось с распространением универсального языка программирования АЛГОЛ-60, допускающего рекурсивные обращения к процедурам. На первых порах аппарат процедур, введенный авторами языка АЛГОЛ, казался необычным и вызывал недоумение. Однако практика показала, что разумное применение рекурсии с последовательным сокращением количественной сложности задач, возникающих в процессе рекурсивных обращений, является весьма эффективным методом программирования, существенно упрощает запись различных сложных алгоритмов, а в ряде случаев оказывается практически незаменимым средством.
Любое рекурсивное описание должно содержать явное определение для некоторых значений аргумента (или аргументов), так как иначе процесс рекурсии оказался бы бесконечным. Для таких описаний удобна запись условного выражения, которую впервые ввел Маккарти. Условные выражения представляются в следующей форме:
[B1->E1,B2->E2,…,Bn-1->En-1,En]
Здесь Bi – логическое условие, которое может быть истиной или ложью, Ei – выражение.
Значение условного выражения получается проверкой значений Bi по очереди слева направо до встречи первого значения "истина". Соответствующее значение Ei берется в качестве значения всего выражения. Если все условия Bi ложны, то выражение принимает значение En.
В качестве примера приведем описание функции для отыскания факториала (n):
factorial (n) =[(n=0)->1,n*factorial(n-1)]
На языке C исходный код имеет вид:
//Программа вычисления факториала с помощью рекурсии
#include<stdio.h>
void main(void)
{
int n=4; // Можно запросить с клавиатуры и проверить на ограничение
long fac(int);
printf("n Факториал%d равен %d",n,fac(n));
}
long fac(int f)
{
if(f==0) return(1); // последнее значение 1
return(f*fac(f-1)); // вычислить факториал (f-1)
}
В общем случае можно утверждать, что рекурсивное использование процедуры или функции требует очевидной конечной глубины рекурсии, тогда как вычисление рекурсивно описанной функции влечет за собой неопределенную глубину рекурсии, зависящую от значений аргументов. Если описание предназначено для практических вычислений, то глубина рекурсии должна быть конечной. Бесконечное по глубине рекурсивное описание называется регрессивным. Некоторые рекурсивные описания могут иметь конечную глубину рекурсии при одних входных данных и бесконечную при других. Теоретически невозможно определять с помощью единого алгоритма, окажется ли произвольное описание конечным в любом случае, однако часто можно показать, будет ли в отдельных случаях глубина рекурсии конечной или бесконечной.
Оба типа рекурсии могут присутствовать одновременно. Наиболее известным примером такого сочетания является функция Аккермана, которая определяется так:
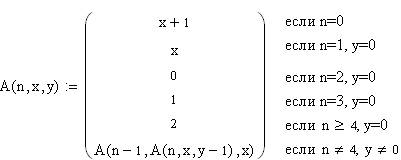
где n,x,y – целые неотрицательные числа.
Следующая программа вычисляет функцию Аккермана с использованием рекурсивной функции ackr и вспомогательной функции smacc:
#include <stdio.h>
#include <conio.h>
void main ()
{
clrscr();
int x,y,n;
long t;
int ackr(int, int, int); // объявление функции ackr
printf(“n Введите 3 целых положительных числа n, x, y:n”);
scanf("%d %d %d",&n,&x,&y);
t=ackr(n,x,y); // подключение функции ackr
printf("Результат вычисления функции Акермана = %ld",t);
getch();
}
int smacc( int n,int x ) // вспомогательная функция
{
switch (n)
{
case 0: return(x+1);
case 1: return (x);
case 2: return (0);
case 3: return (1);
default: return (2);
}
}
int ackr( int n, int x, int y) // рекурсивная функция
{
int z;
int smacc( int,int); // объявление функции smacc
if(n==0 || y==0) z=smacc(n,x);
else
{
z=ackr(n,x,y-1); // рекурсивные вызовы ackr(…)
z=ackr(n-1,z,x);
}
return z;
}
Приведем еще один пример рекурсии. Формула для вычисления числа Фибоначчи имеет вид:
Число n Фибоначчи равно сумме чисел n – 1 и n – 2 для n > 2. Для n<=2 число равно 1. Тогда рекурсивная функция будет иметь вид:
unsignedlongfibonachi(unsignedlongn)
{
if(n==0||n==1)
returnn;
//рекурсивныйшаг
Else
returnfibonachi(n – 1)+fibonachi(n – 2);
}
Ответ на этот вопрос, полезна ли рекурсия, должен зависеть от того, к какой задаче мы собираемся применять рекурсию. Если мы хотим обрабатывать информацию, структура которой описана рекурсивно, то применение рекурсивных методов является необходимым. Например, написать программу копирования списковой структуры, не прибегая к применению рекурсии, затруднительно. Если задача касается процесса, рекурсивного по самой своей природе, то рекурсия опять-таки обязательна, хотя и может быть замаскирована специальными мерами. Поставленный вопрос приобретает смысл только тогда, когда рассматривается применение процесса, не являющегося существенно рекурсивным, к данным, не имеющим рекурсивной внутренней структуры. В таком случае ответ должен зависеть в какой-то степени от того, стремимся ли мы к машинной эффективности или к удобству для пользователя.
Рекурсивную программу можно писать почти прямо по описанию алгоритма, тогда как нерекурсивный вариант требует определенных навыков программирования. Применением рекурсии обеспечивается не только более простое написание программы, но и гораздо более легкое понимание программы пользователями, не участвовавшими в ее разработке.
Однако рекурсивные программы выполняются существенно медленнее, чем нерекурсивные, из-за расходов времени, связанных с организаций стека. Следует отметить, что если рекурсивная программа содержит ошибки, то ее отладка может оказаться весьма затруднительной, особенно если используется глубокая рекурсия. Трудность отладки рекурсивных программ всегда будет оставаться неудобством их применения. Разумеется, нельзя рекомендовать применять рекурсию повсеместно. Программист должен оценить, насколько целесообразно облегчить работу по написанию программы, подвергая себя при этом опасности усложнить отладку и резко увеличить время счета.
Широкое применение рекурсия получила при написании компиляторов. В настоящее время она является для разработчиков компиляторов стандартным приемом. Известно много примеров использования рекурсии в компиляторах.