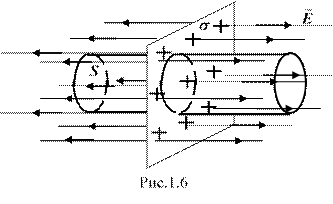
 Бесконечная плоскость (рис. 1.6) заряжена с постоянной поверхностной плотностью +s (s = dQ/dS – заряд, приходящийся на единицу поверхности). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (cosa = 0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь
Бесконечная плоскость (рис. 1.6) заряжена с постоянной поверхностной плотностью +s (s = dQ/dS – заряд, приходящийся на единицу поверхности). Линии напряженности перпендикулярны рассматриваемой плоскости и направлены от нее в обе стороны. В качестве замкнутой поверхности мысленно построим цилиндр, основания которого параллельны заряженной плоскости, а ось перпендикулярна ей. Так как образующие цилиндра параллельны линиям напряженности (cosa = 0), то поток вектора напряженности сквозь боковую поверхность цилиндра равен нулю, а полный поток сквозь цилиндр равен сумме потоков сквозь
его основания (площади оснований равны, и для основания ![]() совпадает с
совпадает с ![]() ), т.е. равен
), т.е. равен ![]() . Заряд, заключенный внутри построенной цилиндрической поверхности, равен sS. Согласно теореме Гаусса (1.1),
. Заряд, заключенный внутри построенной цилиндрической поверхности, равен sS. Согласно теореме Гаусса (1.1), ![]() , откуда
, откуда
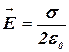 , (1.2)
, (1.2)
где s – поверхностная плотность заряда; e0 – электрическая постоянная.
Из формулы (1.2) вытекает, что ![]() не зависит от длины цилиндра, т.е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно.
не зависит от длины цилиндра, т.е. напряженность поля на любых расстояниях одинакова по модулю, иными словами, поле равномерно заряженной плоскости однородно.