 Бесконечный цилиндр радиуса R (рис. 1.8) заряжен равномерно с линейной плотностью t (
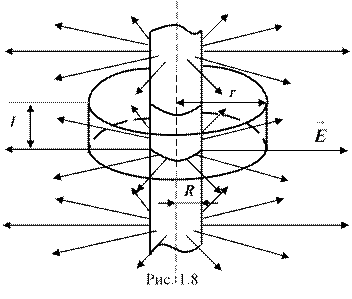
Бесконечный цилиндр радиуса R (рис. 1.8) заряжен равномерно с линейной плотностью t (![]() – заряд, приходящийся на единицу длины). Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим коаксиальный заряженный цилиндр радиуса r и высотой l. Поток вектора
– заряд, приходящийся на единицу длины). Из соображений симметрии следует, что линии напряженности будут направлены по радиусам круговых сечений цилиндра с одинаковой густотой во все стороны относительно оси цилиндра. В качестве замкнутой поверхности мысленно построим коаксиальный заряженный цилиндр радиуса r и высотой l. Поток вектора ![]() сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность равен
сквозь торцы коаксиального цилиндра равен нулю (торцы параллельны линиям напряженности), а сквозь боковую поверхность равен ![]() .
.
По теореме Гаусса (1.1), при r > R ![]() , откуда
, откуда
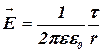
![]() (r ³ R). (1.4)
(r ³ R). (1.4)
Здесь t – линейная плотность заряда; r – радиус цилиндра; e – диэлектрическая проницаемость среды; e0 – электрическая постоянная.
Если r < R, то замкнутая поверхность зарядов внутри не содержит, поэтому в этой области ![]() = 0. Таким образом, напряженность поля вне равномерно заряженного бесконечного цилиндра определяется выражением (1.15), внутри же его поле отсутствует.
= 0. Таким образом, напряженность поля вне равномерно заряженного бесконечного цилиндра определяется выражением (1.15), внутри же его поле отсутствует.