Выражение для силы Лоренца (2.1) позволяет найти ряд закономерностей движения заряженных частиц в магнитном поле. Направление силы Лоренца зависит от знака заряженной частицы.

Если заряженная частица движется в магнитном поле со скоростью  вдоль линий магнитной индукции, то угол a между векторами  и  равен 0 или p. Тогда по формуле (2.1) сила Лоренца равна нулю, и частица движется равномерно и прямолинейно.

Если заряженная частица движется в магнитном поле со скоростью , перпендикулярной вектору , то сила Лоренца равна: ;постоянна по модулю и нормальна к траектории частицы. Согласно второму закону Ньютона, эта сила создает центростремительное ускорение. Из условия  следует, что радиус окружности равен:

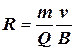.                                                          (2.2)

Период вращения частицы, т.е. время (Т), за которое она совершает один полный оборот, равно:

.

Подставим сюда выражение (2.2) получим:

,

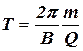т.е. период вращения частицы в однородном магнитном поле не зависит от скорости (при ) и определяется только величиной, обратной удельному заряду () частицы и магнитной индукцией поля.

Если скорость () заряженной частицы направлена под углом a к вектору , то ее движение можно представить в виде суперпозиции:

1) равномерного прямолинейного движения;

2) равномерного движения по окружности в плоскости, перпендикулярной магнитному полю.

В результате сложения обоих движений возникает движение по спирали, ось которой параллельна магнитному полю.