Колеблющееся тело может одновременно участвовать в нескольких колебательных процессах:
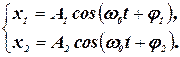
Сложение гармонических колебаний одного направления и одинаковой частоты производится методом вращающегося вектора амплитуды.
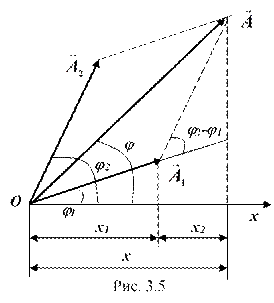 Векторные диаграммы этих колебаний изображены на рис. 3.5. Так как векторы
Векторные диаграммы этих колебаний изображены на рис. 3.5. Так как векторы ![]() и
и ![]() вращаются с одинаковой угловой скоростью w0, то разность фаз (j1 – j2) между ними остается постоянной. Уравнение результирующего колебания будет иметь вид:
вращаются с одинаковой угловой скоростью w0, то разность фаз (j1 – j2) между ними остается постоянной. Уравнение результирующего колебания будет иметь вид:
![]() ,
,
где амплитуда результирующего колебания определяется по формуле: ![]() ; начальная фаза результирующего колебания равна:
; начальная фаза результирующего колебания равна: 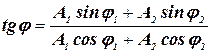 .
.
Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (j2 – j1) складываемых колебаний:
1) j2 – j1 = ±2mp (m = 0, 1, 2, …), А = А1 + А2,
2) j2 – j1 = ±(2m + 1)p (m = 0, 1, 2, …), А = ½А1 – А2½.
Для практики особый интерес представляет случай, когда два складываемых колебания одинакового направления мало отличаются по частоте. В результате сложения этих колебаний получаются колебания с периодически изменяющейся амплиту дой – биения.
Уравнения двух колебаний с амплитудами А и близкими частотами w и w + Dw, причем Dw << w, можно представить в виде:
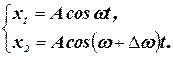
Уравнение результирующего колебания, с учетом того, что Dw/2 << w будет иметь вид:
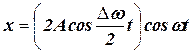 . (3.9)
. (3.9)
Результирующее колебание (3.9) можно рассматривать как гармоническое с частотой w, амплитуда которого изменяется по периодическому закону:
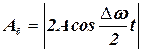 . (3.10)
. (3.10)
Частота изменения Аб в два раза больше частоты изменения косинуса (так как берется по модулю), т.е. частота биений равна разности частот складываемых колебаний:
![]() .
.
 Период биений равен:
Период биений равен:
![]() .
.
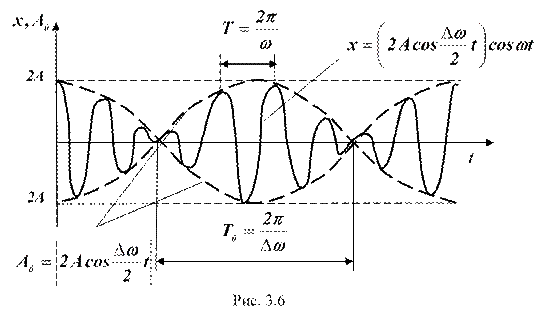
Характер зависимости (3.9) показан на рис. 3.6, где сплошные жирные линии представляют собой график результирующего колебания (3.9), а огибающая их ли ния – график, меняющийся по уравнению (3.10) амплитуды.