Рассмотрим сложение двух взаимно перпендикулярных колебаний вдоль осей х и у одинаковой частоты w:
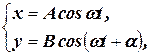 (3.11)
(3.11)
где a – разность фаз складываемых колебаний, А и В – амплитуды складываемых колебаний.
Решением уравнения (3.11) является уравнение эллипса, оси которого ориентированы относительно координатных осей произвольно:
![]() .
.
Так как траектория результирующего колебания имеет форму эллипса, то такие колебания называются эллиптически поляризованными.
Ориентация эллипса и размеры его осей зависят от амплитуд складываемых колебаний и разности фаз a:
1) a = mp (m = 0, ±1, ±2, …). В данном случае эллипс вырождается в отрезок прямой:
![]() .
.
2) a = (2m + 1)p/2 (m = 0, ±1, ±2, …). В данном случае уравнение примет вид:
![]() .
.
Это уравнение эллипса, оси которого совпадают с осями координат и в случае А = В эллипс вырождается в окружность. Такие колебания называются циркулярно поляризованными или колебаниями, поляризованными по кругу.
Если частоты складываемых взаимно перпендикулярных колебаний различны, то замкнутая траектория результирующего колебания довольно сложна. Замкнутые траектории колеблющейся точки, совершающей одновременно два взаимно перпендикулярных колебания, называются фигурами Лиссажу. Вид этих кривых зависит от соотношения амплитуд, частот и разности фаз складываемых колебаний.