В общем случае уравнение плоской волны (волновой поверхностью является плоскость), распространяющейся вдоль положительного направления оси х в среде, не поглощающей энергию, имеет вид:

,                                   (3.12)

где А = const – амплитуда волны; w – циклическая частота; j₀ – начальная фаза волны;  – фаза плоской волны.

Для характеристики волн используется волновое число

.                                                (3.13)

С учётом (3.12) и (3.13) уравнение плоской волны примет вид:

.

Основываясь на формуле Эйлера, уравнение плоской волны можно записать в виде:

.

Аналогично плоской волне, уравнение сферической волны (волновой поверхностью является концентрическая сфера) записывается в виде:

,

где r – расстояние от центра волны до рассматриваемой точки среды. В случае сферической волны даже в среде, не поглощающей энергию, амплитуда колебаний не остается постоянной, а убывает с расстоянием по закону 1/r. Уравнение справедливо лишь для r, значительно превышающих размеры источника (когда источник колебаний можно считать точечным).

Распространение волн в однородной изотропной среде в общем случае описывается волновым уравнением – дифференциальным уравнением в частных производных:

,

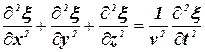или

,                                                     (3.14)

где v – фазовая скорость; 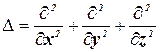 – оператор Лапласа.