Пример 1. На экране наблюдается интерференционная картина в результате наложения лучей от двух когерентных источников (l = 500 нм). На пути одного из лучей перпендикулярно ему поместили стеклянную пластинку (n = 1,6) толщиной d = 5 мкм. Определить, на сколько полос сместится при этом интерференционная картина?
Дано: l = 500 нм = 5×10-7 м, n = 1,6 d = 5 мкм = 5×10-6 м.
Определить: m
Решение. При внесении стеклянной пластинки оптическая разность хода между лучами изменится на ![]() где d – толщина пластинки; n– показатель преломления.
где d – толщина пластинки; n– показатель преломления.
С другой стороны, внесение пластинки приведет к смещению интерференционной картины на m полос, т.е. дополнительная разность хода равна ml. Следовательно,
![]()
откуда найдем искомое m:
![]() .
.
 Подставив числовые значения, получим: m = 6.
Подставив числовые значения, получим: m = 6.
Пример 2. На стеклянный клин (n = 1,5) с преломляющим углом a = 40¢¢ нормально падает монохроматический свет с длиной волны l = 600 нм. Определить в интерференционной картине расстояние между двумя соседними минимумами.
Дано: n = 1,5; a = 40¢¢ = 1,94×10-4 рад; l = 600 нм = 6×10-7 м.
Определить: b.
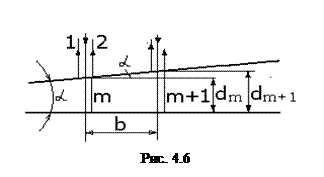
Решение. Параллельный пучок света, падая нормально к грани клина, отражается от его верхней и нижней грани (рис 4.6). Так как угол клина мал, то отраженные лучи 1 и 2 практически параллельны. Отраженные лучи когерентны, и на поверхности клина будут наблюдаться интерференционные полосы параллельные ребру клина.
Условия минимума для клина в общем случае:
![]() , m = 0, 1, 2,…
, m = 0, 1, 2,…
где d – толщина клина вместе темной полосы, соответствующей номеру m; r – угол преломления; l2 – дополнительная разность хода, обусловленная
отражением световой волны 1 от оптически более плотной среды.
Угол падения равен нулю r = 0 (по условию). Тогда условие минимума запишется в виде:
![]() ,
,
откуда ![]() .
.
Из рис. 4.6 следует, что ![]()
Из-за малости угла sina » a, подставив в последнюю формулу толщины dm+1 и dm, получим:
![]()
откуда найдем искомое расстояние между соседними минимумами:
![]()
(a выражается в радианах).
Вычисляя, получим b = 1,03 мм